题目内容
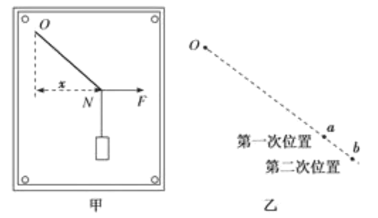
【题目】如图所示,竖直面上有一半径较大的圆弧轨道,最低点为M点,有三个小球A、B、C(可视为质点),A球位于圆心处,B球位于弦轨道MN的顶端N点,C球位于圆弧轨道上极其靠近M的地方。现将三个小球同时由静止释放,不计一切摩擦阻力和空气阻力,则( )

A.C球最先到达M点
B.B球最后到达M点
C.ABC三球同时到达M点
D.条件不足,无法判断哪个小球最先、最后到达M点
【答案】B
【解析】
设圆弧的半径为R,对于A球,做自由落体运动,则有
![]()
解得
![]()
对于B球,沿弦轨道MN做初速度为零的匀加速度直线运动,设弦轨道MN与水平切线的夹角为![]() ,根据几何关系有
,根据几何关系有
![]()
根据牛顿第二定律可得加速度为
![]()
根据位移时间公式有
![]()
解得
![]()
对于C球做单摆运动,根据单摆的运动规律,则有
![]()
综上分析可得
![]()
故B球最后达到M点,A球最先到达M点,故B正确,ACD错误。
故选B。

练习册系列答案
相关题目