题目内容
1.将两完全相同的玩具车A、B并排放在一平直的水平上,分别通过挂钩拉着另一个等质量的玩具拖车,控制两车以相同的速度 v0做匀速直线运动.某一时刻,通过控制器使两车连接拖车的挂钩同时断开,玩具车A保持原来的牵引力不变前进,玩具车B保持原来的输出功率不变前进,当玩具车A的速度为2v0时,玩具车B的速度为1.5v0,已知水平面对两车的阻力均为车重的0.1倍,g=10m/s2,则从挂钩断开至A、B两车的速度分别为2v0和1.5v0的 过程中,下列说法正确的是( )| A. | A、B两车的位移之比为12:11 | |
| B. | 玩具车A的速度为2v0时其功率为此时玩具车B功率的4倍 | |
| C. | 两车所受水平面的阻力做功的比值为11:12 | |
| D. | 两车牵引力做功的比值为3:2 |
分析 先研究两车匀速运动的过程,求得牵引力和功率.从挂钩断开至A、B两车的速度分别为2v0和1.5v0的过程中,对A,运用牛顿第二定律和运动学公式研究位移.对B,运用动能定理研究位移,从而求得位移之比.由P=Fv求玩具车A的速度为2v0时的功率,即可求得两车功率之比.由功的计算公式求阻力做功的比值.由W=Fl求牵引力对A车做的功,由W=Pt求牵引力对B车做的功.从而求得牵引力做功之比.
解答 解:A、设玩具车A、B的质量为m.匀速运动时,两玩具车的牵引力 F=2×0.1mg=0.2mg,输出功率 P=F•v0=0.2mgv0.
从挂钩断开至A车的速度为2v0的过程中,加速度为 a=$\frac{F-0.1mg}{m}$=0.1g,用时 t=$\frac{2{v}_{0}-{v}_{0}}{a}$=$\frac{{v}_{0}}{0.1g}$=$\frac{10{v}_{0}}{g}$,位移 xA=$\frac{{v}_{0}+2{v}_{0}}{2}t$=$\frac{15{v}_{0}^{2}}{g}$
从挂钩断开至B车的速度为1.5v0的过程中,由动能定理得:Pt-0.1mgxB=$\frac{1}{2}m(1.5{v}_{0})^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
解得B的位移 xB=$\frac{55{v}_{0}^{2}}{4g}$,所以 xA:xB=$\frac{15{v}_{0}^{2}}{g}$:$\frac{55{v}_{0}^{2}}{4g}$=12:11.故A正确.
B、玩具车A的速度为2v0时其功率为 PA=F•2v0=0.4mgv0,B车的功率为 P=F•v0=0.2mgv0.所以玩具车A的速度为2v0时其功率为此时玩具车B功率的2倍,故B错误.
C、两车所受水平面的阻力做功的比值为 WfA:WfB=-fxA:(-fxB)=12:11,故C错误.
D、两车牵引力做功的比值 WFA:WFB=FxA:Pt=(0.2mg•$\frac{15{v}_{0}^{2}}{g}$):(0.2mgv0•$\frac{10{v}_{0}}{g}$)=3:2,故D正确.
故选:AD
点评 本题是机车起动问题,要抓住两种起动方式中车子的运动情况,运用牛顿第二定律和运动学公式研究匀加速运动的位移,对于B车的变加速运动,不能根据运动学公式求位移,要根据动能定理求位移.

| A. | m1=m2,r1>r2 | B. | m1>m2,r1=r2 | ||
| C. | 降低斜槽的高度 | D. | 入射小球释放点要适当高一些 |
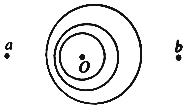
| A. | 该波源正在移向a点 | B. | 该波源正在移向b点 | ||
| C. | 在b处观察,波的频率变低 | D. | 在a处观察,波的频率变低 |
 如图所示为一个质点做匀变速曲线运动的轨迹示意图,已知在B点的速度与加速度相互垂直,则下列说法中正确的是( )
如图所示为一个质点做匀变速曲线运动的轨迹示意图,已知在B点的速度与加速度相互垂直,则下列说法中正确的是( )| A. | E点的速率比D点的速率大 | B. | A点的加速度与速度的夹角小于90° | ||
| C. | A点的加速度比D点的加速度大 | D. | 图中各点中,B点速度最小 |
 如图,电阻不计足够长的两金属导轨平行倾斜放置,与水平面的夹角θ=30°,导轨间距为l,处于方向垂直于导轨平面强度为B的匀强磁场中.长度均为l的导体棒ab和cd垂直跨放在导轨上.ab棒的质量为m、电阻为r,与导轨间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$.cd棒光滑,质量为2m、电阻为r.开始两棒均位于导轨顶端,现由静止同时释放两棒,当cd棒下滑的距离为x时,ab棒开始运动.设最大静摩擦力等于滑动摩擦力,重力加速度为g.求:
如图,电阻不计足够长的两金属导轨平行倾斜放置,与水平面的夹角θ=30°,导轨间距为l,处于方向垂直于导轨平面强度为B的匀强磁场中.长度均为l的导体棒ab和cd垂直跨放在导轨上.ab棒的质量为m、电阻为r,与导轨间的动摩擦因数μ=$\frac{\sqrt{3}}{2}$.cd棒光滑,质量为2m、电阻为r.开始两棒均位于导轨顶端,现由静止同时释放两棒,当cd棒下滑的距离为x时,ab棒开始运动.设最大静摩擦力等于滑动摩擦力,重力加速度为g.求: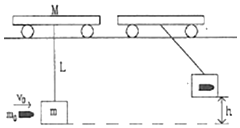 如图所示,质量为M的天车静止在光滑轨道上,下面用长为L的细绳悬挂着质量为m的沙箱,一颗质量为m0的子弹,以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求沙箱上升的最大高度.
如图所示,质量为M的天车静止在光滑轨道上,下面用长为L的细绳悬挂着质量为m的沙箱,一颗质量为m0的子弹,以v0的水平速度射入沙箱,并留在其中,在以后运动过程中,求沙箱上升的最大高度.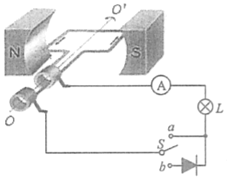 如图所示,一匝数为N=100匝的矩形线圈,面积S=0.0lm2,内阻不计,绕垂直于磁感线的对称轴OO′匀速转动.设线圈经过的磁场为匀强磁场,磁感应强度B=$\frac{\sqrt{2}}{10}$T,线圈通过滑环接一标有“6V 3W”
如图所示,一匝数为N=100匝的矩形线圈,面积S=0.0lm2,内阻不计,绕垂直于磁感线的对称轴OO′匀速转动.设线圈经过的磁场为匀强磁场,磁感应强度B=$\frac{\sqrt{2}}{10}$T,线圈通过滑环接一标有“6V 3W”