题目内容
6.一个质量m=2kg的物体在水平拉力F的作用下,在光滑水平面上从静止开始做匀加速直线运动,经过时间t=6s的位移x=54m.求:(1)物体的加速度a的大小;
(2)水平拉力F的大小.
分析 (1)根据加速度的定义式求出加速度;
(2)根据牛顿第二定律求出水平拉力.
解答 解:(1)根据匀变速直线运动位移公式x=$\frac{1}{2}$at2得:54=$\frac{1}{2}$×a×62
解得:a=3m/s2
(2)对物体受力分析,物体受到重力、支持力和水平拉力,竖直方向上受力平衡.
根据牛顿第二定律可得:F=ma=2×3=6N
答:(1)物体的加速度大小为3m/s2;
(2)水平拉力大小为6N.
点评 应用牛顿运动定律结合运动学方程解决的简单问题,较容易.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
16.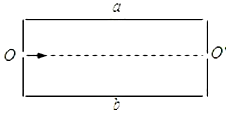 图中为一“滤速器”装置示意图,a、b 为水平放置的平行金属板,一束具有 各种不同速率的电子沿水平方向经小孔 O 进入 a、b 两板之间.为了选取具有某 种特定速率的电子,可在 a、b 间加上电压,并沿垂直于纸面的方向加一匀强磁 场,使所选 电子仍能够沿水平直线 OO'运动,由 O'射出.不计重力作用.可能 达到上述目的办法是( )
图中为一“滤速器”装置示意图,a、b 为水平放置的平行金属板,一束具有 各种不同速率的电子沿水平方向经小孔 O 进入 a、b 两板之间.为了选取具有某 种特定速率的电子,可在 a、b 间加上电压,并沿垂直于纸面的方向加一匀强磁 场,使所选 电子仍能够沿水平直线 OO'运动,由 O'射出.不计重力作用.可能 达到上述目的办法是( )
 图中为一“滤速器”装置示意图,a、b 为水平放置的平行金属板,一束具有 各种不同速率的电子沿水平方向经小孔 O 进入 a、b 两板之间.为了选取具有某 种特定速率的电子,可在 a、b 间加上电压,并沿垂直于纸面的方向加一匀强磁 场,使所选 电子仍能够沿水平直线 OO'运动,由 O'射出.不计重力作用.可能 达到上述目的办法是( )
图中为一“滤速器”装置示意图,a、b 为水平放置的平行金属板,一束具有 各种不同速率的电子沿水平方向经小孔 O 进入 a、b 两板之间.为了选取具有某 种特定速率的电子,可在 a、b 间加上电压,并沿垂直于纸面的方向加一匀强磁 场,使所选 电子仍能够沿水平直线 OO'运动,由 O'射出.不计重力作用.可能 达到上述目的办法是( )| A. | 使 a 板电势高于 b 板,磁场方向垂直纸面向里 | |
| B. | 使 a 板电势低于 b 板,磁场方向垂直纸面向里 | |
| C. | 使 a 板电势高于 b 板,磁场方向垂直纸面向外 | |
| D. | 使 a 板电势低于 b 板,磁场方向垂直纸面向外 |
17.将一个小球从20m的塔顶以20m/s的速度水平抛出,忽略空气阻力,重力加速度取10m/s2,则下落到地面的时间是( )
| A. | 10s | B. | 5s | C. | 2s | D. | 1s |
14.一个质点在做曲线运动,下列说法正确的是( )
| A. | 速度一定在不断改变,加速度也一定不断改变 | |
| B. | 质点不可能在做匀变速运动 | |
| C. | 若该质点做圆周运动,其加速度是变化的,方向一定指向圆心 | |
| D. | 质点速度方向在时刻变化,一定在做变速运动 |
1.将两完全相同的玩具车A、B并排放在一平直的水平上,分别通过挂钩拉着另一个等质量的玩具拖车,控制两车以相同的速度 v0做匀速直线运动.某一时刻,通过控制器使两车连接拖车的挂钩同时断开,玩具车A保持原来的牵引力不变前进,玩具车B保持原来的输出功率不变前进,当玩具车A的速度为2v0时,玩具车B的速度为1.5v0,已知水平面对两车的阻力均为车重的0.1倍,g=10m/s2,则从挂钩断开至A、B两车的速度分别为2v0和1.5v0的 过程中,下列说法正确的是( )
| A. | A、B两车的位移之比为12:11 | |
| B. | 玩具车A的速度为2v0时其功率为此时玩具车B功率的4倍 | |
| C. | 两车所受水平面的阻力做功的比值为11:12 | |
| D. | 两车牵引力做功的比值为3:2 |
11.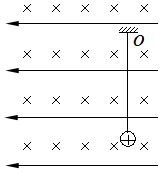 如图所示,在正交的匀强电场和匀强磁场中,电场方向水平向左,磁场方向垂直于纸面水平向里,一质量为m,带电量为+q的小球用长为L的绝缘细线悬挂于O点,并在最低点由静止释放,小球向左摆到最高点时,悬线与竖直方向的夹角为θ,不计小球的大小和空气阻力,重力加速度为g,则下列说法正确的是( )
如图所示,在正交的匀强电场和匀强磁场中,电场方向水平向左,磁场方向垂直于纸面水平向里,一质量为m,带电量为+q的小球用长为L的绝缘细线悬挂于O点,并在最低点由静止释放,小球向左摆到最高点时,悬线与竖直方向的夹角为θ,不计小球的大小和空气阻力,重力加速度为g,则下列说法正确的是( )
 如图所示,在正交的匀强电场和匀强磁场中,电场方向水平向左,磁场方向垂直于纸面水平向里,一质量为m,带电量为+q的小球用长为L的绝缘细线悬挂于O点,并在最低点由静止释放,小球向左摆到最高点时,悬线与竖直方向的夹角为θ,不计小球的大小和空气阻力,重力加速度为g,则下列说法正确的是( )
如图所示,在正交的匀强电场和匀强磁场中,电场方向水平向左,磁场方向垂直于纸面水平向里,一质量为m,带电量为+q的小球用长为L的绝缘细线悬挂于O点,并在最低点由静止释放,小球向左摆到最高点时,悬线与竖直方向的夹角为θ,不计小球的大小和空气阻力,重力加速度为g,则下列说法正确的是( )| A. | 电场强度的大小为$\frac{mgtanθ}{q}$ | |
| B. | 小球从释放到摆到左侧最高点的过程中,电势能减小了 | |
| C. | 小球从释放到摆到左侧最高点的过程中,当悬线与竖直方向的夹角为$\frac{θ}{2}$时,悬线拉力最大 | |
| D. | 增大悬线的长度,θ会增大 |
18.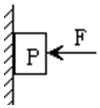 如图所示,物体P用水平作用力F压在竖直的墙上,沿墙匀速下滑,物体的重力为G,墙对物体的弹力为FN、摩擦力为Ff,物体对墙的压力FN′摩擦力为Ff′.下列说法正确的有( )
如图所示,物体P用水平作用力F压在竖直的墙上,沿墙匀速下滑,物体的重力为G,墙对物体的弹力为FN、摩擦力为Ff,物体对墙的压力FN′摩擦力为Ff′.下列说法正确的有( )
 如图所示,物体P用水平作用力F压在竖直的墙上,沿墙匀速下滑,物体的重力为G,墙对物体的弹力为FN、摩擦力为Ff,物体对墙的压力FN′摩擦力为Ff′.下列说法正确的有( )
如图所示,物体P用水平作用力F压在竖直的墙上,沿墙匀速下滑,物体的重力为G,墙对物体的弹力为FN、摩擦力为Ff,物体对墙的压力FN′摩擦力为Ff′.下列说法正确的有( )| A. | G 和Ff′是一对平衡力 | B. | FN和F是一对作用力和反作用力 | ||
| C. | Ff和Ff′是一对作用力和反作用力 | D. | F 就是FN′ |
16.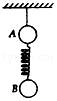 如图所示,质量均为m的A、B两球,用细线相连,然后利用轻弹簧将它们悬挂在天花板下方,待它们静止后剪短细线,则剪断瞬间( )
如图所示,质量均为m的A、B两球,用细线相连,然后利用轻弹簧将它们悬挂在天花板下方,待它们静止后剪短细线,则剪断瞬间( )
 如图所示,质量均为m的A、B两球,用细线相连,然后利用轻弹簧将它们悬挂在天花板下方,待它们静止后剪短细线,则剪断瞬间( )
如图所示,质量均为m的A、B两球,用细线相连,然后利用轻弹簧将它们悬挂在天花板下方,待它们静止后剪短细线,则剪断瞬间( )| A. | A、B两球的加速度大小均为2g | |
| B. | A球的加速度大小为2g,B球的加速度大小为0 | |
| C. | A球的加速度大小为0,B球的加速度大小为2g | |
| D. | A、B两球的加速度大小均为0 |
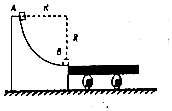 如图所示,半径R=0.45m的光滑圆弧轨道固定在竖直平面内,B为轨道的最低点,在光滑的水平面上紧挨B点有一静止的小平板车,平板车质量M=2kg,长度为L=0.5m,小车的上表面与B点等高,质量m=1kg的物块(可视为质点)从圆弧最高点A由静止释放.g取10m/s2.试求:
如图所示,半径R=0.45m的光滑圆弧轨道固定在竖直平面内,B为轨道的最低点,在光滑的水平面上紧挨B点有一静止的小平板车,平板车质量M=2kg,长度为L=0.5m,小车的上表面与B点等高,质量m=1kg的物块(可视为质点)从圆弧最高点A由静止释放.g取10m/s2.试求: