题目内容
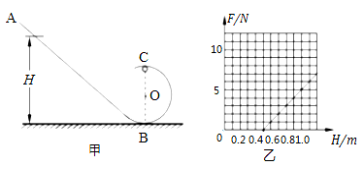
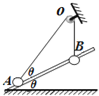
【题目】如图所示,轨道ABCD的AB段为一半径R=0.2 m的光滑1/4圆形轨道,BC段为高为h=5 m的竖直轨道,CD段为水平轨道.一质量为0.2 kg的小球从A点由静止开始下滑,到达B点时速度的大小为2 m/s,离开B点做平抛运动(g=10 m/s2),求:
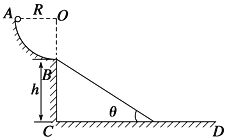
(1)小球离开B点后,在CD轨道上的落地点到C点的水平距离;
(2)小球到达B点时对圆形轨道的压力大小;
(3)如果在BCD轨道上放置一个倾角θ=45°的斜面(如图中虚线所示),那么小球离开B点后能否落到斜面上?如果能,求它第一次落在斜面上的位置距离B点有多远.如果不能,请说明理由.
【答案】(1)2 m (2)6 N (3)能落到斜面上,第一次落在斜面上的位置距离B点1.13 m
【解析】(1)根据h=![]() gt2得,
gt2得, ![]() ,
,
则落地点与C点的水平距离x=vBt=2×1m=2m.
(2)根据动能定理得,mgR=![]() mvB2,
mvB2,
解得![]() ,
,
根据牛顿第二定律得, ![]() ,
,
解得![]() ,
,
由牛顿第三定律知小球到达B点时对圆形轨道的压力大小为6 N,方向竖直向下.
(3)如图,斜面BEC的倾角θ=45°,CE长d=h=5 m,因为d>x,所以小球离开B点后能落在斜面上;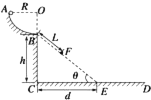
假设小球第一次落在斜面上F点,BF长为L,小球从B点到F点的时间为t2;
Lcos θ=vBt2 ①
![]() ②
②
联立①②两式得t2=0.4 s;L≈1.13 m.

【题目】在测量电源的电动势和内阻的实验中,由于所用电压表(视为理想电压表)的量程较小,某同学设计了如图所示的实物电路。
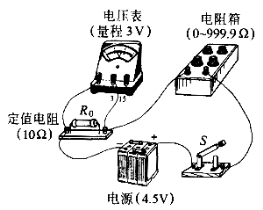
(1)实验时,应先将电阻箱的电阻调到_______(选填“最大值”、“最小值”或“任意值”)。
(2)改变电阻箱的阻值R,分别测出阻值R0=10Ω的定值电阻两端的电压U。下列表格中两组R的取值方案中,比较合理的方案是_______(选填“1”或“2”)。
方案编号 | 电阻箱的阻值R(Ω) | ||||
1 | 400.0 | 350.0 | 300.0 | 250.0 | 200.0 |
2 | 80.0 | 70.0 | 60.0 | 50.0 | 40.0 |
(3)根据实验数据描点,绘出的![]() -R图像是一条直线,若直线的斜率为k,在
-R图像是一条直线,若直线的斜率为k,在![]() 坐标轴上的截距为b,则该电源的电动势E=______,内阻r=_____。(用k、b和R0表示)
坐标轴上的截距为b,则该电源的电动势E=______,内阻r=_____。(用k、b和R0表示)