题目内容
8.地球半径为R,地球表面的重力加速度为g,若高处某处的重力加速度为$\frac{g}{3}$,则该处距地面的高度为( )| A. | 3R | B. | $\frac{3}{2}$R | C. | $\sqrt{3}$R | D. | ($\sqrt{3}$-1)R |
分析 地球表面的物体所受的重力,可以近似看做等于地球对其的万有引力,根据万有引力等于重力列式求解.
解答 解:设地球的质量为M,物体质量为m,物体距地面的高度为h.根据万有引力近似等于重力,在地球表面,有:
mg=G$\frac{Mm}{R^{2}}$
在高度为h处,有:m•$\frac{g}{3}$=G$\frac{Mm}{(R+h)^{2}}$
联立解得:h=($\sqrt{3}$-1)R,故D正确,ABC错误.
故选:D.
点评 本题关键要知道重力与万有引力的关系,明确在不考虑地球自转的情况下万有引力近似等于重力,知道重力加速度与高度的关系,并能用来分析实际问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 弹性介质中波源O沿竖直方向振动产生的振幅为0.1m的简谐横波以速度v=10m/s传播,M、N为与O在同一直线上的两质点,它们到O的距离分别为OM=12m、ON=6m.波源O开始振动一段时间后在直线MN上形成的波形如图所示,波刚好传到M点,不计波传播过程中的能量损失.下列说法正确的( )
弹性介质中波源O沿竖直方向振动产生的振幅为0.1m的简谐横波以速度v=10m/s传播,M、N为与O在同一直线上的两质点,它们到O的距离分别为OM=12m、ON=6m.波源O开始振动一段时间后在直线MN上形成的波形如图所示,波刚好传到M点,不计波传播过程中的能量损失.下列说法正确的( )
 弹性介质中波源O沿竖直方向振动产生的振幅为0.1m的简谐横波以速度v=10m/s传播,M、N为与O在同一直线上的两质点,它们到O的距离分别为OM=12m、ON=6m.波源O开始振动一段时间后在直线MN上形成的波形如图所示,波刚好传到M点,不计波传播过程中的能量损失.下列说法正确的( )
弹性介质中波源O沿竖直方向振动产生的振幅为0.1m的简谐横波以速度v=10m/s传播,M、N为与O在同一直线上的两质点,它们到O的距离分别为OM=12m、ON=6m.波源O开始振动一段时间后在直线MN上形成的波形如图所示,波刚好传到M点,不计波传播过程中的能量损失.下列说法正确的( )| A. | 此时O点的振动方向向上 | |
| B. | 波源的振动频率为2.5Hz | |
| C. | 波传播到N时,N先向下振动 | |
| D. | M与N的速度方向始终相同 | |
| E. | 从O开始振动到此时N质点运动的路程为0.6m |
19.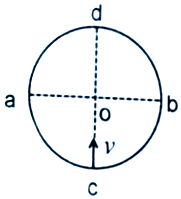 如图所示,在真空中有半径为r=0.1m的圆形区域,圆心为O,ab和cd是两条相互垂直的直径,若区域内有垂直于纸面向外的磁感应强度为B=0.01T的匀强磁场,一束带正电的粒子流连续不断地以速度v=1.0×103m/s,从c点沿cd方向射入场区,带电粒子均经过b点,若再加一水平向左的匀强电场,这束带电粒子将沿cd方向做直线运动,不计粒子重力,下列说法正确的是( )
如图所示,在真空中有半径为r=0.1m的圆形区域,圆心为O,ab和cd是两条相互垂直的直径,若区域内有垂直于纸面向外的磁感应强度为B=0.01T的匀强磁场,一束带正电的粒子流连续不断地以速度v=1.0×103m/s,从c点沿cd方向射入场区,带电粒子均经过b点,若再加一水平向左的匀强电场,这束带电粒子将沿cd方向做直线运动,不计粒子重力,下列说法正确的是( )
 如图所示,在真空中有半径为r=0.1m的圆形区域,圆心为O,ab和cd是两条相互垂直的直径,若区域内有垂直于纸面向外的磁感应强度为B=0.01T的匀强磁场,一束带正电的粒子流连续不断地以速度v=1.0×103m/s,从c点沿cd方向射入场区,带电粒子均经过b点,若再加一水平向左的匀强电场,这束带电粒子将沿cd方向做直线运动,不计粒子重力,下列说法正确的是( )
如图所示,在真空中有半径为r=0.1m的圆形区域,圆心为O,ab和cd是两条相互垂直的直径,若区域内有垂直于纸面向外的磁感应强度为B=0.01T的匀强磁场,一束带正电的粒子流连续不断地以速度v=1.0×103m/s,从c点沿cd方向射入场区,带电粒子均经过b点,若再加一水平向左的匀强电场,这束带电粒子将沿cd方向做直线运动,不计粒子重力,下列说法正确的是( )| A. | 若间该粒子速率变大,粒子将从直径cd的左侧离开磁场 | |
| B. | 若只有匀强磁场,带电粒子在磁场中运动的时间约为1.57×10-4s | |
| C. | 若只有匀强电场,仅改变粒子从c点沿cd方向入射的粒子的速度大小,粒子离开圆形区域时速度反向延长线不可能通过圆心O | |
| D. | 若只有匀强磁场,仅改变粒子在C点的入射方向,经磁场偏转后均水平向右离开磁场 |
3.己知某卫星绕地球做匀速圆周运动,卫星质量为m,距离地球表面高度为h,地球的半径为R,地球表面处的重力加速度为g,下列说法正确的是( )
| A. | 卫星对地球的引力大小为mg | B. | 卫星的向心加速度大小为$\frac{R}{R+h}$g | ||
| C. | 卫星的周期为$\frac{2π(R+h)}{R}$$\sqrt{\frac{R+h}{g}}$ | D. | 卫星的动能为$\frac{mg{R}^{2}}{R+h}$ |
13.如图大致可以反映伽利略对自由落体运动研究的实验和思维过程,对这一过程的分析中正确的是( )


| A. | 甲、乙、丙、丁图均是当时可以测量的实验过程 | |
| B. | 运用甲图的实验,可以直接得到实验结论 | |
| C. | 运用甲图的实验,可“冲淡”重力的作用,使实验现象更明显 | |
| D. | 运用丁图的实验,可“放大”重力的作用,使实验现象更明显 |
20.2016年10月19日凌晨,“神舟十一号”载人飞船与距离地面343km的圆轨道上的“天宫二号”交会对接.已知地球半径为R=6400km,万有引力常量G=6.67×10-11N•m2/kg2,“天宫二号”绕地球飞行的周期为90分钟,以下分析正确的是( )
| A. | “天宫二号”的发射速度应大于11.2km/s | |
| B. | “天宫二号”的向心加速度大于同步卫星的向心加速度 | |
| C. | 由题中数据可以求得地球的平均密度 | |
| D. | “神舟十一号”加速与“天宫二号”对接前应处于同一圆周轨道 |
17.“天上”的力与“人间”的力可能出于同一本源,为了检验这一猜想,牛顿做了著名的“月-地检验”.在牛顿的时代,重力加速度已经能够比较精确地测定,当时也能比较精确地测定月球与地球的距离,月球的公转周期.已知月球与地球之间的距离为3.8×108m,月球的公转周期为27.3天,地球表面的重力加速度g=9.8m/s2,则月球公转的向心加速度a月与重力加速度g的大小之比约为( )
| A. | $\frac{1}{2400}$ | B. | $\frac{1}{3600}$ | C. | $\frac{1}{4800}$ | D. | $\frac{1}{6400}$ |
15. 一列简谐横渡在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.1s第一次到达平衡位置,已知波速为5m/s.则( )
一列简谐横渡在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.1s第一次到达平衡位置,已知波速为5m/s.则( )
 一列简谐横渡在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.1s第一次到达平衡位置,已知波速为5m/s.则( )
一列简谐横渡在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.1s第一次到达平衡位置,已知波速为5m/s.则( )| A. | 该波沿x轴正方向传播 | |
| B. | x=0处质点在t=0时刻振动速度最大 | |
| C. | Q点的振幅比P点大 | |
| D. | P点的横坐标为x=2.5m | |
| E. | 图中Q点(坐标为x=7.5m的点)的振动方程为y=5cos$\frac{5π}{3}$t |
 如图所示,在竖直平面内有足够长的平行金属导轨MN、PQ,其间距为L=2m,在N、Q之间连接由阻值为R=0.8Ω的电阻,一匀强磁场与导轨平面垂直,磁感应强度为B0,现有一细线绕过光滑的轻质定滑轮,一端系一质量为M=3kg的重物,另一端与质量为m=1kg的金属杆相连,金属杆接入两导轨间的电阻为r=0.2Ω,开始时金属杆置于导轨下端NQ处,将重物由静止释放,当重物下降h=5m时恰好达到温度速度v而匀速下降,已知v=5m/s,且运动过程中金属杆始终与导轨垂直且接触良好,不计一切摩擦和导轨电阻,重力加速度g=10m/s2,求:
如图所示,在竖直平面内有足够长的平行金属导轨MN、PQ,其间距为L=2m,在N、Q之间连接由阻值为R=0.8Ω的电阻,一匀强磁场与导轨平面垂直,磁感应强度为B0,现有一细线绕过光滑的轻质定滑轮,一端系一质量为M=3kg的重物,另一端与质量为m=1kg的金属杆相连,金属杆接入两导轨间的电阻为r=0.2Ω,开始时金属杆置于导轨下端NQ处,将重物由静止释放,当重物下降h=5m时恰好达到温度速度v而匀速下降,已知v=5m/s,且运动过程中金属杆始终与导轨垂直且接触良好,不计一切摩擦和导轨电阻,重力加速度g=10m/s2,求: