题目内容
3.我国首个月球探测计划“嫦娥工程”将分三个阶段实施,大约用十年左右时间完成,这极大地提高了同学们对月球的关注程度.以下是某同学就有关月球的知识设计的两个问题,请你解答:(1)若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,且把月球绕地球的运动近似看作是匀速圆周运动.试求出月球绕地球运动的轨道半径.
(2)若某位宇航员随登月飞船登陆月球后,在月球某水平表面上方h高处以速度v0水平抛出一个小球,小球落回到月球表面的水平距离为s.已知月球半径为R月,万有引力常量为G.试求出月球的质量M月.
分析 (1)月球绕地球的运动时,由地球的万有引力提供向心力,由牛顿第二定律列出月球的轨道半径与地球质量等物理量的关系式;物体在地球表面上时,由重力等于地球的万有引力求出地球的质量,再求出月球的轨道半径.
(2)小球在在月球某水平表面上方h高处以速度v0水平抛出一个小球,求出月球表面的重力加速度,根据重力等于万有引力求出月球的质量.
解答 解:(1)地球表面的物体受到的重力等于万有引力:G$\frac{Mm}{{R}^{2}}$=mg,
月球绕地球做圆周运动,万有引力题干向心力,由牛顿第二定律得:G$\frac{M{m}_{月}}{{r}^{2}}$=m月$(\frac{2π}{T})^{2}$r,
解得:r=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$;
(2)小球做平抛运动,
竖直方向:h=$\frac{1}{2}$g月t2,
水平方向:s=0t,
万有引力等于重力:G$\frac{{M}_{月}m}{{R}_{月}^{2}}$=mg月,
解得:M月=$\frac{2h{R}_{月}^{2}{v}_{0}^{2}}{G{s}^{2}}$;
答:(1)球绕地球运动的轨道半径为$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$.
(2)月球的质量M月为$\frac{2h{R}_{月}^{2}{v}_{0}^{2}}{G{s}^{2}}$.
点评 本题是卫星类型的问题,常常建立这样的模型:环绕天体绕中心天体做匀速圆周运动,由中心天体的万有引力提供向心力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.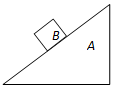 斜劈A静止放置在水平地面上,质量为m的物体B在外力F1和F2的共同作用下沿斜劈表面向下运动.当F1方向水平向右,F2方向沿平行斜劈的表面向下时,斜劈A受到地面的摩擦力方向向左.若斜劈保持静止,下列说法中正确的是( )
斜劈A静止放置在水平地面上,质量为m的物体B在外力F1和F2的共同作用下沿斜劈表面向下运动.当F1方向水平向右,F2方向沿平行斜劈的表面向下时,斜劈A受到地面的摩擦力方向向左.若斜劈保持静止,下列说法中正确的是( )
 斜劈A静止放置在水平地面上,质量为m的物体B在外力F1和F2的共同作用下沿斜劈表面向下运动.当F1方向水平向右,F2方向沿平行斜劈的表面向下时,斜劈A受到地面的摩擦力方向向左.若斜劈保持静止,下列说法中正确的是( )
斜劈A静止放置在水平地面上,质量为m的物体B在外力F1和F2的共同作用下沿斜劈表面向下运动.当F1方向水平向右,F2方向沿平行斜劈的表面向下时,斜劈A受到地面的摩擦力方向向左.若斜劈保持静止,下列说法中正确的是( )| A. | 若同时撤去F1和F2,物体B的加速度方向一定沿斜面向下 | |
| B. | 若只撤去F2,在物体B仍向下运动的过程中,A所受地面摩擦力方向不变 | |
| C. | 改变F1和F2的大小,仍使物体B沿斜劈表面运动,A所受地面摩擦力可能为0 | |
| D. | 若只撤去F1,在物体B仍向下运动的过程中,A所受地面摩擦力方向可能向右 |
15.关于电磁场和电磁波,下列说法正确的有( )
| A. | 电磁波不能在真空中传播 | |
| B. | 变化的电场一定能产生变化的磁场 | |
| C. | 电磁波传播的速度是3×108m/s | |
| D. | 变化的电场和磁场由近及远地向周围空间传播形成电磁波 |
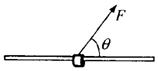 如图,将质量m=0.1kg的圆环套在固定的水平直杆上.环的直径略大于杆的截面直径.环与杆间动摩擦因数μ=0.8.对环施加一位于竖直平面内斜向上,与杆夹角θ=53°的拉力F,使圆环由静止以a=4.4m/s2的加速度沿杆运动,求F的大小可能值(提示:环与杆的接触可能是上部也可能是下部).
如图,将质量m=0.1kg的圆环套在固定的水平直杆上.环的直径略大于杆的截面直径.环与杆间动摩擦因数μ=0.8.对环施加一位于竖直平面内斜向上,与杆夹角θ=53°的拉力F,使圆环由静止以a=4.4m/s2的加速度沿杆运动,求F的大小可能值(提示:环与杆的接触可能是上部也可能是下部).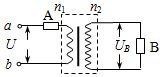 如图所示,理想变压器的原、副线圈匝数之比为n1:n2=4:1,原线圈回路中的电阻A与副线圈回路中的负载电阻B的阻值相等,a、b端加入交流电压U后,通过A、B两电阻电流之比IA:IB=1:4;a、b两端的电压和电阻B两端的电压之比为UA:UB=17:4.
如图所示,理想变压器的原、副线圈匝数之比为n1:n2=4:1,原线圈回路中的电阻A与副线圈回路中的负载电阻B的阻值相等,a、b端加入交流电压U后,通过A、B两电阻电流之比IA:IB=1:4;a、b两端的电压和电阻B两端的电压之比为UA:UB=17:4.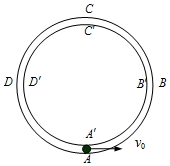 如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD的光滑,内圆A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑.一质量m=0.2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,球运动的半径R=0.2m,取g=10m/s2.
如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD的光滑,内圆A′B′C′D′的上半部分B′C′D′粗糙,下半部分B′A′D′光滑.一质量m=0.2kg的小球从轨道的最低点A,以初速度v0向右运动,球的尺寸略小于两圆间距,球运动的半径R=0.2m,取g=10m/s2.