题目内容
13.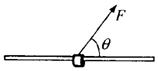 如图,将质量m=0.1kg的圆环套在固定的水平直杆上.环的直径略大于杆的截面直径.环与杆间动摩擦因数μ=0.8.对环施加一位于竖直平面内斜向上,与杆夹角θ=53°的拉力F,使圆环由静止以a=4.4m/s2的加速度沿杆运动,求F的大小可能值(提示:环与杆的接触可能是上部也可能是下部).
如图,将质量m=0.1kg的圆环套在固定的水平直杆上.环的直径略大于杆的截面直径.环与杆间动摩擦因数μ=0.8.对环施加一位于竖直平面内斜向上,与杆夹角θ=53°的拉力F,使圆环由静止以a=4.4m/s2的加速度沿杆运动,求F的大小可能值(提示:环与杆的接触可能是上部也可能是下部).
分析 根据平衡条件可求得恰好没有挤压时的拉力大小,再分别对上端挤压和下端挤压两种情况进行分析,根据牛顿第二定律列式即可求得F的大小.
解答 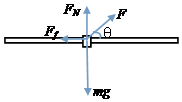 解:若球与杆之间没有相互压力,则有Fsin53°-mg=0,
解:若球与杆之间没有相互压力,则有Fsin53°-mg=0,
解得F=1.25N.
当F<1.25N时,环与杆的上部接触,受力如图.
由牛顿第二定律,Fcosθ-μFN=ma,
Fsinθ+FN=mg,
联立解得:F=$\frac{m(a+μg)}{cosθ+μsinθ}$
代入数据得:F=1N.
当F>1.25N时,环与杆的下部接触,受力如图.
由牛顿第二定律,Fcosθ-μFN=ma,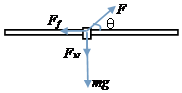
Fsinθ=mg+FN,
联立解得:F=$\frac{m(a-μg)}{cosθ-μsinθ}$
代入数据得:F=9N.
答:F的大小可能值为1N和9N.
点评 本题考查牛顿第二定律的应用,要注意明确本题中可能存在的两种情况,明确拉力过大时,物体受杆下部的挤压,而拉力较小时,受杆上端的挤压,要求能找出这两种情况才能全面分析求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.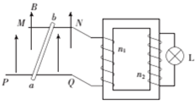 如图所示,水平面上放置有间距为0.5m的平行金属导轨MN和PQ,并处于竖直向上的匀强磁场中,在金属导轨上放置光滑导体棒ab.N、Q端分别与一理想变压器原线圈相连,理想变压器副线圈接有“5V、0.1A”的小灯泡L0导体棒ab在外力F作用下运动,其速度随时间变化的规律为v=$\sqrt{2}$sin(10πt)m/s,小灯泡恰能正常发光,选取向左为正方向,已知原副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{1}{5}$,导体棒和导线的电阻都不计,则下列说法正确的是( )
如图所示,水平面上放置有间距为0.5m的平行金属导轨MN和PQ,并处于竖直向上的匀强磁场中,在金属导轨上放置光滑导体棒ab.N、Q端分别与一理想变压器原线圈相连,理想变压器副线圈接有“5V、0.1A”的小灯泡L0导体棒ab在外力F作用下运动,其速度随时间变化的规律为v=$\sqrt{2}$sin(10πt)m/s,小灯泡恰能正常发光,选取向左为正方向,已知原副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{1}{5}$,导体棒和导线的电阻都不计,则下列说法正确的是( )
 如图所示,水平面上放置有间距为0.5m的平行金属导轨MN和PQ,并处于竖直向上的匀强磁场中,在金属导轨上放置光滑导体棒ab.N、Q端分别与一理想变压器原线圈相连,理想变压器副线圈接有“5V、0.1A”的小灯泡L0导体棒ab在外力F作用下运动,其速度随时间变化的规律为v=$\sqrt{2}$sin(10πt)m/s,小灯泡恰能正常发光,选取向左为正方向,已知原副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{1}{5}$,导体棒和导线的电阻都不计,则下列说法正确的是( )
如图所示,水平面上放置有间距为0.5m的平行金属导轨MN和PQ,并处于竖直向上的匀强磁场中,在金属导轨上放置光滑导体棒ab.N、Q端分别与一理想变压器原线圈相连,理想变压器副线圈接有“5V、0.1A”的小灯泡L0导体棒ab在外力F作用下运动,其速度随时间变化的规律为v=$\sqrt{2}$sin(10πt)m/s,小灯泡恰能正常发光,选取向左为正方向,已知原副线圈匝数比$\frac{{n}_{1}}{{n}_{2}}$=$\frac{1}{5}$,导体棒和导线的电阻都不计,则下列说法正确的是( )| A. | 磁感应强度B=$\sqrt{2}$T | B. | 磁感应强度B=2T | ||
| C. | 通过灯泡交流电的频率为5Hz | D. | 通过导体棒的电流大小为0.02A |
4.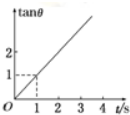 某物体做平抛运动时,它的速度方向与水平方向的夹角为θ,其正切值tanθ随时间t变化的图象如图所示,则(g取10m/s2)( )
某物体做平抛运动时,它的速度方向与水平方向的夹角为θ,其正切值tanθ随时间t变化的图象如图所示,则(g取10m/s2)( )
 某物体做平抛运动时,它的速度方向与水平方向的夹角为θ,其正切值tanθ随时间t变化的图象如图所示,则(g取10m/s2)( )
某物体做平抛运动时,它的速度方向与水平方向的夹角为θ,其正切值tanθ随时间t变化的图象如图所示,则(g取10m/s2)( )| A. | 第1 s物体下落的高度为5 m | B. | 第1 s物体下落的高度为10 m | ||
| C. | 物体的初速度为5 m/s | D. | 物体的初速度是10 m/s |
1.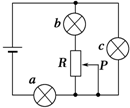 在如图所示的电路中,a、b、c为三个相同的灯泡,其电阻值均大于电源内阻,当变阻器R的滑动触头P向上移动时,下列判断中正确的是( )
在如图所示的电路中,a、b、c为三个相同的灯泡,其电阻值均大于电源内阻,当变阻器R的滑动触头P向上移动时,下列判断中正确的是( )
 在如图所示的电路中,a、b、c为三个相同的灯泡,其电阻值均大于电源内阻,当变阻器R的滑动触头P向上移动时,下列判断中正确的是( )
在如图所示的电路中,a、b、c为三个相同的灯泡,其电阻值均大于电源内阻,当变阻器R的滑动触头P向上移动时,下列判断中正确的是( )| A. | b灯变暗,a、c灯变亮 | B. | a、b、c灯泡全变亮 | ||
| C. | 电源输出功率增大 | D. | 电源的供电效率增大 |
8.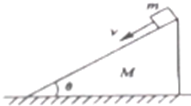 如图所示,放置在水平地面上的直角劈M上有一个质量m的物体,若m在其上匀速下滑,M仍保持静止,那么正确的说法是( )
如图所示,放置在水平地面上的直角劈M上有一个质量m的物体,若m在其上匀速下滑,M仍保持静止,那么正确的说法是( )
 如图所示,放置在水平地面上的直角劈M上有一个质量m的物体,若m在其上匀速下滑,M仍保持静止,那么正确的说法是( )
如图所示,放置在水平地面上的直角劈M上有一个质量m的物体,若m在其上匀速下滑,M仍保持静止,那么正确的说法是( )| A. | M对地面的压力等于(M+m)g | B. | M对地面的压力大于(M+m)g | ||
| C. | 地面对M没有摩擦力 | D. | 地面对M有向左的摩擦力 |
18.关于声现象,下列说法正确的是( )
| A. | 声音是由于物体振动产生的 | |
| B. | 声源的振幅越大,音调越高 | |
| C. | 声音在真空中的传播速度是3×108m/s | |
| D. | 超声波的频率很低,所以人耳听不到 |