题目内容
9.银是电阻率很小的导电体,假设银导线中50%的银原子的最外层电子脱离原子核的束缚而成为自由电子.①求银导线中自由电子的数密度(即单位体积内银导线中自由电子的个数).
②一根直径为d=2.0mm的银导线中通过的电流为I=0.40A,求银导线中自由电子定向移动的平均速率.(计算时取银的密度ρ=1.0×104kg/m3,银的摩尔质量M=0.10kg/mol,阿伏加德罗常量NA=6.0×1023/mol,电子电荷量e=1.6×10-19C.计算结果保留2位有效数字.)
分析 ①根据m=ρV,结合银的密度,可知,1 m3的质量,从而确定其摩尔数,再求得含有银原子的个数N,再根据ρe=$\frac{50%N}{V}$,即可求解.
②根据直径求出导线的横截面积,再由电流的微观表达式求自由电子定向移动的平均速率.
解答 解.①1 m3银导线的质量为:m=ρV=1.0×104kg,
这些银的物质的量 为:n=$\frac{m}{M}$=$\frac{1.0×1{0}^{4}}{0.10}$=1.0×105mol,
含有的银原子数为:N=n•NA=1.0×105×6.0×1023=6.0×1028(个).
银导线中自由电子数密度为为:ρe=$\frac{50%N}{V}$=$\frac{0.5×6.0×1{0}^{28}}{1}$=3.0×1028/m3.
②导线的横截面积为:S=π($\frac{d}{2}$)2=3.14×($\frac{0.002}{2}$)2≈3.1×10-6m2.
设导线中自由电子的平均速率为v,根据I=ρe•vS•e,得:v=$\frac{I}{{ρ}_{e}Se}$=$\frac{0.40}{3.0×1{0}^{28}×3.1×1{0}^{-6}×1.6×1{0}^{-19}}$m/s≈2.7×10-5m/s.
答:①银导线中自由电子数密度为3.0×1028/m3.
②银导线中自由电子定向移动的平均速率是2.7×10-5m/s.
点评 本题建立正确的物理模型是解题的关键,要在理解的基础上掌握阿伏加德罗常数的意义和电流的微观表达式,解题时要注意保留两位有效数字.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
4.不带电的金属导体P与带正电的金属导体Q接触之后也带正电,原因是( )
| A. | P有部分电子转移到Q上 | B. | Q有部分电子转移到P上 | ||
| C. | P有部分正电荷转移到Q上 | D. | Q有部分正电荷转移到P上 |
4.我们研究的带电粒子是指那些受到的电场力远大于重力的粒子.下列粒子不能忽略重力的是( )
| A. | 电子 | B. | 质子 | C. | 氧离子 | D. | 带电小球 |
1. 如图所示电路中,电源电动势为E、内阻为r,R0为定值电阻,电容器的电容为C.闭合开关S,增大可变电阻R的阻值,电压表示数的变化量为△U,电流表示数的变化量为△I,则( )
如图所示电路中,电源电动势为E、内阻为r,R0为定值电阻,电容器的电容为C.闭合开关S,增大可变电阻R的阻值,电压表示数的变化量为△U,电流表示数的变化量为△I,则( )
 如图所示电路中,电源电动势为E、内阻为r,R0为定值电阻,电容器的电容为C.闭合开关S,增大可变电阻R的阻值,电压表示数的变化量为△U,电流表示数的变化量为△I,则( )
如图所示电路中,电源电动势为E、内阻为r,R0为定值电阻,电容器的电容为C.闭合开关S,增大可变电阻R的阻值,电压表示数的变化量为△U,电流表示数的变化量为△I,则( )| A. | 变化过程中△U和△I的比值将会增加 | |
| B. | 电压表示数U和电流表示数I的比值不变 | |
| C. | 电阻R0两端电压减小,减小量为△U | |
| D. | 电容器的带电量增大,增加量为C△U |
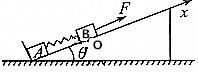 如图所示,倾角为θ的光滑斜面的底端固定一垂直于斜面的挡板,质量同为m的A、B两物体由劲度系数为k的轻弹簧连接,放在斜面上,最初处于静止状态.现用一平行于斜面的力F拉B物体沿斜面向上缓慢运动,在物体A离开挡板之前(弹簧一直处于弹性限度内),B物块沿斜面上升的位移l和此时F的大小是$\frac{2mgsinθ}{k}$、2mgsinθ.
如图所示,倾角为θ的光滑斜面的底端固定一垂直于斜面的挡板,质量同为m的A、B两物体由劲度系数为k的轻弹簧连接,放在斜面上,最初处于静止状态.现用一平行于斜面的力F拉B物体沿斜面向上缓慢运动,在物体A离开挡板之前(弹簧一直处于弹性限度内),B物块沿斜面上升的位移l和此时F的大小是$\frac{2mgsinθ}{k}$、2mgsinθ. 如图所示电路中,电源电动势E=6.00V,其内阻忽略不计.电阻的阻值分别为R1=2.4kΩ、R2=4.8kΩ,电容器的电容C=4.7μF.闭合开关S,待电路中的电流稳定后,电容器两板间的电压为4V;电容器所带的电量是2.82×10-5C.
如图所示电路中,电源电动势E=6.00V,其内阻忽略不计.电阻的阻值分别为R1=2.4kΩ、R2=4.8kΩ,电容器的电容C=4.7μF.闭合开关S,待电路中的电流稳定后,电容器两板间的电压为4V;电容器所带的电量是2.82×10-5C.