题目内容
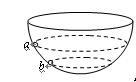
如图所示，一根长为L的细杆的一端固定一质量为m的小球，整个系统绕杆的另一端在竖直面内做圆周运动，且小球恰能过最高点。已知重力加速度为g，细杆的质量不计。下列说法正确的是
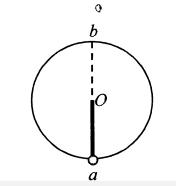
A．小球过最低点时的速度大小为 |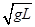
| B．小球过最高点时的速度大小为 |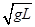
| C．小球过最低点时受到杆的拉力大小为5mg |
| D．小球过最高点时受到杆的支持力为零 |
C
试题分析：因杆能支撑小球，轻杆带着物体做圆周运动，只要物体能够到达最高点就可以了，所以小球恰能过最高点时，在最高点的速度为零，所以B错误；设小球过最低点的速度为
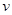，小球从最高点到达最低点的过程中，只有重力做功，机械能守恒，则有
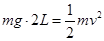，解得：
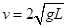，故A错误；在最高点和最低点时球的重力与杆对球的作用力的合力提供向心力．以小球为研究对象，设在最低点时杆对小球的作用力大小为
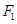，方向竖直向上，根据牛顿第二定律得，
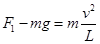，解得：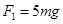
，故C正确；以小球为研究对象，设在最高点时杆对小球的作用力大小为F，方向竖直向上，小球刚好能通过最高点P，速度为零，根据牛顿第二定律得，
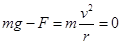，即有F=mg，所以小球过最高点时受到杆的支持力大小为
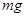，方向竖直向上，故D错误．所以选C．
练习册系列答案
相关题目
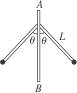
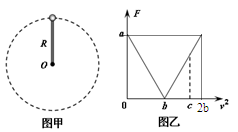
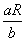
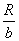
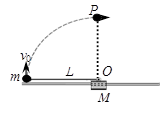
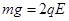，若仍从A点由静止释放该小球，则（ ）
