题目内容
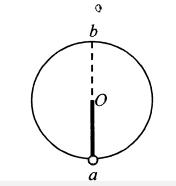
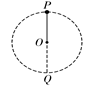
如图所示，物体P用两根长度相等不可伸长的细线系于竖直杆上，它们随杆转动，若转动角速度为ω，则下列说法错误的是
| A．ω只有超过某一值时，绳子AP才有拉力 |
| B．线BP的拉力随ω的增大而增大 |
| C．线BP的拉力一定大于线AP的拉力 |
| D．当ω增大到一定程度时，线AP的拉力将大于BP的拉力 |
D
试题分析：设BP绳与竖直方向的夹角为
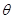，AP绳与竖直方向的夹角为
，对物体P进行受力分析，根据向心力公式则有：
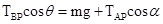… ①
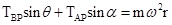…②当ω较小时，BP绳在水平方向的分量可以提供向心力，此时AP绳没有力，当ω增加到某值时，BP绳在水平方向的分量不足以提供向心力，此时绳子AP才有力的作用，故A正确；
ω的增大，所需的向心力增大，绳子BP和AP的力都增大，故B正确；
当AP绳子没有拉直时，AP绳拉力等于零，BP绳肯定有拉力，当AP绳拉直时，θ=α，由①式可知，绳BP的张力一定大于绳子AP的张力，故C正确，D错误；
让选错误的，故选D
点评：本题的关键是对物体P进行受力分析，知道用正交分解法求出物体P分别在水平、竖直两个方向受到的合力
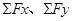，由牛顿运动定律布列方程，
分析讨论，难度适中．
练习册系列答案
相关题目
