题目内容
14.火星可视为半径为r 的均匀球体,它的一个卫星绕火星运行的圆轨道半径为R,周期为T.求:(1)火星的质量.(万有引力常量为G)
(2)火星表面的重力加速度.
(3)在火星表面离地h处以水平速度v0抛出的物体,落地时速度多大.(不计火星空气阻力)
分析 卫星绕火星做圆周运动受到的万有引力提供向心力,列出等式求出火星的质量;
根据万有引力等于重力求解火星表面的重力加速度.
根据动能定理求解落地时速度.
解答 解:(1)卫星绕火星做圆周运动受到的万有引力提供向心力,列出等式
G$\frac{mM}{{R}^{2}}$=m$\frac{{4π}^{2}R}{{T}^{2}}$
解得:M=$\frac{{{4π}^{2}R}^{3}}{{GT}^{2}}$,
(2)根据火星表面万有引力等于重力得
$\frac{GMm}{{r}^{2}}$=mg
解得:g=$\frac{GM}{{r}^{2}}$=$\frac{{{4π}^{2}R}^{3}}{{{T}^{2}r}^{2}}$
(3)在火星表面离地h处以水平速度v0抛出的物体,
根据动能定理得
mgh=$\frac{1}{2}$mv2-$\frac{1}{2}$m${v}_{0}^{2}$
解得:v=$\sqrt{2gh{+v}_{0}^{2}}$=$\sqrt{\frac{8h{{π}^{2}R}^{3}}{{{T}^{2}r}^{2}}{+v}_{0}^{2}}$
答:(1)火星的质量是$\frac{{{4π}^{2}R}^{3}}{{GT}^{2}}$;
(2)火星表面的重力加速度是$\frac{{{4π}^{2}R}^{3}}{{{T}^{2}r}^{2}}$.
(3)在火星表面离地h处以水平速度v0抛出的物体,落地时速度是$\sqrt{\frac{8h{{π}^{2}R}^{3}}{{{T}^{2}r}^{2}}{+v}_{0}^{2}}$.
点评 解决本题的关键掌握万有引力提供向心力和万有引力等于重力这两个理论,并能熟练运用.

练习册系列答案
相关题目
9. 如图所示为皮带传动装置,主动轮O1上两轮的半径为3r和r,从动轮O2的半径为2r,A、B、C分别为轮缘上的三点,设皮带轮不打滑,则A、B、C三点的角速度之比ωA:ωB:ωC为( )
如图所示为皮带传动装置,主动轮O1上两轮的半径为3r和r,从动轮O2的半径为2r,A、B、C分别为轮缘上的三点,设皮带轮不打滑,则A、B、C三点的角速度之比ωA:ωB:ωC为( )
 如图所示为皮带传动装置,主动轮O1上两轮的半径为3r和r,从动轮O2的半径为2r,A、B、C分别为轮缘上的三点,设皮带轮不打滑,则A、B、C三点的角速度之比ωA:ωB:ωC为( )
如图所示为皮带传动装置,主动轮O1上两轮的半径为3r和r,从动轮O2的半径为2r,A、B、C分别为轮缘上的三点,设皮带轮不打滑,则A、B、C三点的角速度之比ωA:ωB:ωC为( )| A. | 1:1:2 | B. | 2:2:1 | C. | 3:1:2 | D. | 3:3:2 |
19.从距地面某一高度水平抛出一小石子,空气阻力不计,下列说法正确的是( )
| A. | 抛出点高度越大,石子在空中飞行时间越小 | |
| B. | 石子竖直方向的分速度与时间成正比 | |
| C. | 石子竖直方向的分位移与时间成正比 | |
| D. | 石子在空中的速度方向与竖直方向的夹角逐渐变大 |
3. 如图所示,A、B两物体靠在一起静止放在粗糙水平面上,质量分别为mA=1kg,mB=4kg,A、B与水平面间的滑动摩擦因数均为0.6,g取10m/s2,若用水平力FA=6N推A物体.则下列有关说法正确的是( )
如图所示,A、B两物体靠在一起静止放在粗糙水平面上,质量分别为mA=1kg,mB=4kg,A、B与水平面间的滑动摩擦因数均为0.6,g取10m/s2,若用水平力FA=6N推A物体.则下列有关说法正确的是( )
 如图所示,A、B两物体靠在一起静止放在粗糙水平面上,质量分别为mA=1kg,mB=4kg,A、B与水平面间的滑动摩擦因数均为0.6,g取10m/s2,若用水平力FA=6N推A物体.则下列有关说法正确的是( )
如图所示,A、B两物体靠在一起静止放在粗糙水平面上,质量分别为mA=1kg,mB=4kg,A、B与水平面间的滑动摩擦因数均为0.6,g取10m/s2,若用水平力FA=6N推A物体.则下列有关说法正确的是( )| A. | A对B的水平推力为6N | |
| B. | B物体受5个力作用 | |
| C. | A物体受到水平面向左的摩擦力,大小为6N | |
| D. | 若FA变为40N,则A对B的推力为20N |
 如图所示,一根长为L=0.4m的直导线放在水平方向的匀强磁场中,导线水平且与磁场方向垂直,导线中通有向右的电流.
如图所示,一根长为L=0.4m的直导线放在水平方向的匀强磁场中,导线水平且与磁场方向垂直,导线中通有向右的电流. 在“研究平抛物体的运动”的实验中
在“研究平抛物体的运动”的实验中 在静止的车厢内,用细绳a和b系住一个小球,绳a斜向上拉,绳b水平拉,如图所示.现让车从静止开始向右做匀加速运动,小球相对于车厢的位置不变,与小车静止时相比,绳a、b的拉力变化情况是Fa不变,Fb变小 (填变大,变小或不变).
在静止的车厢内,用细绳a和b系住一个小球,绳a斜向上拉,绳b水平拉,如图所示.现让车从静止开始向右做匀加速运动,小球相对于车厢的位置不变,与小车静止时相比,绳a、b的拉力变化情况是Fa不变,Fb变小 (填变大,变小或不变).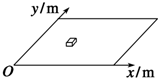 如图所示,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,已知物体运动过程中的坐标与时间的关系为$\left\{\begin{array}{l}{x=3.0t米}\\{y=0.2{t}^{2}米}\end{array}\right.$,t是以s为单位的数值.g=10m/s2.根据以上条件,求:
如图所示,质量m=2.0kg的物体在水平外力的作用下在水平面上运动,已知物体运动过程中的坐标与时间的关系为$\left\{\begin{array}{l}{x=3.0t米}\\{y=0.2{t}^{2}米}\end{array}\right.$,t是以s为单位的数值.g=10m/s2.根据以上条件,求: 如图所示,一长L=0.8m的水平传送带以恒定的速度3m/s做顺时针运动.传送带离地面的高度h=1.25m,其右侧地面上有一直径D=0.5m的圆形洞,洞口最左端的A点离传送带右端的水平距离x=2m,B点在洞口的最右端.现使一小物块以v0=2m/s的速度向右水平滑上传送带(图中未画出),传送带与小物块之间的动摩擦因数μ=0.5,g取10m/s2.
如图所示,一长L=0.8m的水平传送带以恒定的速度3m/s做顺时针运动.传送带离地面的高度h=1.25m,其右侧地面上有一直径D=0.5m的圆形洞,洞口最左端的A点离传送带右端的水平距离x=2m,B点在洞口的最右端.现使一小物块以v0=2m/s的速度向右水平滑上传送带(图中未画出),传送带与小物块之间的动摩擦因数μ=0.5,g取10m/s2.