题目内容
15. 如图所示,两木块M、N从固定斜面顶端沿左边和右边同时由静止滑下,且两术块与斜面间的动摩擦因数相同,图中α+β=90°且α>β.则关于两物块沿斜面下滑过程的说法正确的是( )
如图所示,两木块M、N从固定斜面顶端沿左边和右边同时由静止滑下,且两术块与斜面间的动摩擦因数相同,图中α+β=90°且α>β.则关于两物块沿斜面下滑过程的说法正确的是( )| A. | M的加速度比N的加速度大 | |
| B. | M在斜面上运动的时间更长 | |
| C. | M到达水平地面时的速度比N到达水平地面时的速度大 | |
| D. | M克服摩擦力所做的功必比N克服摩擦力所做的功小 |
分析 根据牛顿第二定律和位移时间公式研究两个物体在斜面上运动的加速度关系和时间关系,由功的公式可分析克服摩擦力所做的功,根据动能定理可分析两个物体到达水平地面时的速度大小关系.
解答 解:A、木块M在斜面上下滑的过程,根据牛顿第二定律得 mgsinα-μmgcosα=maM,得 aM=gsinα-μgcosα.同理可得,木块N在斜面上下滑的加速度大小 aN=gsinβ-μgcosβ;由于α>β,sinα>sinβ,cosα<cosβ,所以aM>aN.故A正确;
B、由$\frac{h}{sinα}$=$\frac{1}{2}$at2可得:t=$\sqrt{\frac{2h}{asinα}}$=$\sqrt{\frac{2h}{(gsinα-μgcosα)sinα}}$;同理可知,N滑下时所用时间t'=$\sqrt{\frac{2h}{asinαβ}}$=$\sqrt{\frac{2h}{(gsinβ-μgcosβ)sinβ}}$;因sinα=cosβ,且sinα>sinβ,则可知,t<t',故M在斜面上运动的时间更短,故B错误;
C、根据动能定理得:mgh-μmgcosα$\frac{h}{sinα}$=$\frac{1}{2}$mv2,得 v=$\sqrt{2gh-μg\frac{h}{tanα}}$,同理可知,N滑下的速度为v’=$\sqrt{2gh-μg\frac{h}{tanβ}}$;因α>β,故tanα>tanβ,故v大于v′,故C正确;
D、克服摩擦力做功为:W=μmgcosα$\frac{h}{sinα}$=$\frac{μmgh}{tanα}$,同理可知,N克服摩擦力做功为W‘=$\frac{μmgh}{tanβ}$:因α>β,故tanα>tanβ,故在M面上克服摩擦力做功小,故D正确.
故选:ACD.
点评 本题运用牛顿第二定律、动能定理及运动学公式结合来分析加速度、速度和时间的关系,这是常用的方法.运用动能定理时,要灵活选择研究的过程.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案| A. | 经典物理学可视为相对论在低速运动时的特例 | |
| B. | 真空中的光速在不同的惯性参考系中是不相同的 | |
| C. | 一条沿自身长度方向运动的杆,其长度总比杆静止时的长度大 | |
| D. | 狭义相对论全面否定了经典物理学 |
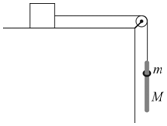 一物块置于水平桌面上,一端系于物块的轻绳平行于桌面绕过光滑的轻质定滑轮,轻绳的另一端系一质量为M的杆,杆自然下垂,杆上穿有质量为m(m<M)的小环,如图所示.重力加速度大小为g.当小环以加速度a沿杆加速下滑时,物块仍保持静止,则物块受到桌面的摩擦力可能为( )
一物块置于水平桌面上,一端系于物块的轻绳平行于桌面绕过光滑的轻质定滑轮,轻绳的另一端系一质量为M的杆,杆自然下垂,杆上穿有质量为m(m<M)的小环,如图所示.重力加速度大小为g.当小环以加速度a沿杆加速下滑时,物块仍保持静止,则物块受到桌面的摩擦力可能为( )| A. | (M+m)g | B. | Mg | C. | (M+m)g-ma | D. | (M+m)g-Ma |
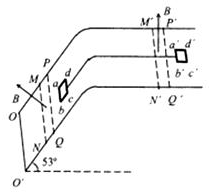 如图所示,倾角53°的绝缘斜面与绝缘水平面平滑对接,斜面及水平面上的矩形区域MNPQ、M′N′P′Q′内有磁感应强度大小均为B,方向垂直于各自表面向上的匀强磁场,磁场宽度$\overline{NQ}$=$\overline{N′Q′}$=L.abcd、a′b′c′d′是两个完全相间的正方形导线框,其质量均为m、边长均为L,两框通过不可伸长的绝缘轻线相连后,分别置子于斜面和水平面上,ab∥a′b′∥MN∥M′N′∥OO′.开始时 锁定a′b′c′d′框,此时ab与PQ、a′b′与P′Q′的距离也为L.解除锁定,两框一起运动,恰好能匀速通过磁场.己知两框与表面的动摩檫因数均为0.25.不计轻线与表面的摩擦,重力加速度为g.sin53°=0.8,cos53°=0.6,下列判断正确的是( )
如图所示,倾角53°的绝缘斜面与绝缘水平面平滑对接,斜面及水平面上的矩形区域MNPQ、M′N′P′Q′内有磁感应强度大小均为B,方向垂直于各自表面向上的匀强磁场,磁场宽度$\overline{NQ}$=$\overline{N′Q′}$=L.abcd、a′b′c′d′是两个完全相间的正方形导线框,其质量均为m、边长均为L,两框通过不可伸长的绝缘轻线相连后,分别置子于斜面和水平面上,ab∥a′b′∥MN∥M′N′∥OO′.开始时 锁定a′b′c′d′框,此时ab与PQ、a′b′与P′Q′的距离也为L.解除锁定,两框一起运动,恰好能匀速通过磁场.己知两框与表面的动摩檫因数均为0.25.不计轻线与表面的摩擦,重力加速度为g.sin53°=0.8,cos53°=0.6,下列判断正确的是( )| A. | 刚进入磁场时,ab边感应电流的方向由a至b | |
| B. | 刚进入磁场时,abcd框克服安培力做功的功率为$\frac{13mg\sqrt{10gL}}{100}$ | |
| C. | 两导线框的电阻均为$\frac{{B}^{2}{L}^{2}}{mg}$$\sqrt{10gl}$ | |
| D. | 从开始运动到cd边刚好离开磁场,经历的时间为2$\sqrt{\frac{10L}{g}}$ |
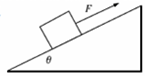 如图所示,一个物体在沿斜面向上的恒力F作用下,由静止从光滑斜面的底端沿斜面向上做匀加速运动,经时间t力F做功为60J,此后撤去恒力F,物体又经时间t回到出发点,若以地面为零势能面,则下列说法正确的是( )
如图所示,一个物体在沿斜面向上的恒力F作用下,由静止从光滑斜面的底端沿斜面向上做匀加速运动,经时间t力F做功为60J,此后撤去恒力F,物体又经时间t回到出发点,若以地面为零势能面,则下列说法正确的是( )| A. | 物体回到出发点的动能为60J | |
| B. | 开始时物体所受恒力F=2mgsinθ | |
| C. | 撤去力F时,物体重力势能是45J | |
| D. | 运动后,动能与势能相等位置在撤去力F的位置的下方 |
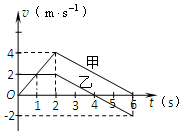 甲、乙两个物体从同一地点、沿同一直线同时做直线运动,其v-t图象如图所示,则下列说法错误的是( )
甲、乙两个物体从同一地点、沿同一直线同时做直线运动,其v-t图象如图所示,则下列说法错误的是( )| A. | 2s时甲和乙相遇 | B. | 2~6s内甲相对乙做匀速直线运动 | ||
| C. | 2~6s内乙的加速度保持不变 | D. | 0~6s内甲乙相距最大距离为4m |
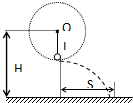 如图所示,用细线把小球悬挂在墙壁的钉子O上,小球绕悬点O在竖直平面内做圆周运动.小球质量为2kg,绳长L为0.8m,悬点距地面高度为1.6m.小球运动至最低点时,绳恰好被拉断,小球着地时速度与水平成45°,当地重力加速度为10m/s2.求:
如图所示,用细线把小球悬挂在墙壁的钉子O上,小球绕悬点O在竖直平面内做圆周运动.小球质量为2kg,绳长L为0.8m,悬点距地面高度为1.6m.小球运动至最低点时,绳恰好被拉断,小球着地时速度与水平成45°,当地重力加速度为10m/s2.求: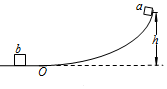 如图所示,光滑的轨道固定在竖直平面内,其O点左边为水平轨道,O点右边的曲线轨道高度h=0.80m,左右两段轨道在O点平滑连接.质量m=0.10kg的小滑块a由静止开始从曲线轨道的顶端沿轨道下滑,到达水平段后与处于静止状态的质量M=0.20kg的小滑块b发生碰撞,碰撞后小滑块a恰好停止运动.取重力加速度g=10m/s2,求:
如图所示,光滑的轨道固定在竖直平面内,其O点左边为水平轨道,O点右边的曲线轨道高度h=0.80m,左右两段轨道在O点平滑连接.质量m=0.10kg的小滑块a由静止开始从曲线轨道的顶端沿轨道下滑,到达水平段后与处于静止状态的质量M=0.20kg的小滑块b发生碰撞,碰撞后小滑块a恰好停止运动.取重力加速度g=10m/s2,求: 如图所示,“冰雪游乐场”滑道O点的左边为水平滑道,右边为高度h=3.2m的曲面滑道,左右两边的滑道在O点平滑连接.小孩乘坐冰车由静止开始从滑道顶端出发,经过O点后与处于静止状态的家长所坐的冰车发生碰撞,碰撞后小孩及其冰车恰好停止运动.已知小孩和冰车的总质量m=30kg,家长和冰车的总质量为M=60kg,人与冰车均可视为质点,不计一切摩擦阻力,取重力加速度g=10m/s2,求:
如图所示,“冰雪游乐场”滑道O点的左边为水平滑道,右边为高度h=3.2m的曲面滑道,左右两边的滑道在O点平滑连接.小孩乘坐冰车由静止开始从滑道顶端出发,经过O点后与处于静止状态的家长所坐的冰车发生碰撞,碰撞后小孩及其冰车恰好停止运动.已知小孩和冰车的总质量m=30kg,家长和冰车的总质量为M=60kg,人与冰车均可视为质点,不计一切摩擦阻力,取重力加速度g=10m/s2,求: