题目内容
10. 如图所示,“冰雪游乐场”滑道O点的左边为水平滑道,右边为高度h=3.2m的曲面滑道,左右两边的滑道在O点平滑连接.小孩乘坐冰车由静止开始从滑道顶端出发,经过O点后与处于静止状态的家长所坐的冰车发生碰撞,碰撞后小孩及其冰车恰好停止运动.已知小孩和冰车的总质量m=30kg,家长和冰车的总质量为M=60kg,人与冰车均可视为质点,不计一切摩擦阻力,取重力加速度g=10m/s2,求:
如图所示,“冰雪游乐场”滑道O点的左边为水平滑道,右边为高度h=3.2m的曲面滑道,左右两边的滑道在O点平滑连接.小孩乘坐冰车由静止开始从滑道顶端出发,经过O点后与处于静止状态的家长所坐的冰车发生碰撞,碰撞后小孩及其冰车恰好停止运动.已知小孩和冰车的总质量m=30kg,家长和冰车的总质量为M=60kg,人与冰车均可视为质点,不计一切摩擦阻力,取重力加速度g=10m/s2,求:(1)小孩乘坐冰车经过O点时的速度大小;
(2)碰撞后家长和冰车共同运动的速度大小;
(3)碰撞过程中小孩和家长(包括各自冰车)组成的系统损失的机械能.
分析 (1)小孩乘坐冰车由曲面下滑的过程,只有重力做功,其机械能守恒,由机械能守恒定律求小孩乘坐冰车经过O点时的速度大小;
(2)对于碰撞过程,小孩和家长(包括各自冰车)组成的系统动量守恒,由动量守恒定律求碰撞后家长和冰车共同运动的速度大小;
(3)碰撞过程中小孩和家长(包括各自冰车)组成的系统损失的机械能等于碰撞前后机械能的差,由能量守恒定律求解.
解答 解:(1)设小孩经过O点时的速度大小为v0,小孩乘坐冰车由曲面下滑的过程,由机械能守恒定律有
$mgh=\frac{1}{2}mv_0^2$
解得:v0=$\sqrt{2gh}$=$\sqrt{2×10×3.2}$=8m/s
(2)碰撞过程中小孩和家长(包括各自冰车)组成的系统动量守恒,设碰撞后家长的速度大小为v1,取向左为正方向,由动量守恒定律得
mv0=Mv1
解得 v1=$\frac{m}{M}$v0=$\frac{30}{60}$×8=4m/s
(3)设系统损失的机械能为△E,则 $△E=\frac{1}{2}mv_0^2-\frac{1}{2}Mv_1^2$=$\frac{1}{2}×30×{8}^{2}$-$\frac{1}{2}×60×{4}^{2}$=480J
答:
(1)小孩乘坐冰车经过O点时的速度大小是8m/s;
(2)碰撞后家长和冰车共同运动的速度大小是4m/s;
(3)碰撞过程中小孩和家长(包括各自冰车)组成的系统损失的机械能是480J.
点评 解决本题的关键是明确碰撞的基本规律:动量守恒定律.要知道当曲面光滑时,往往根据机械能守恒定律求物体的速度.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
1.2017年,中国航天最大的看点应属嫦娥五号,根据计划,我国将在今年11月底前后发射嫦娥五号探测器,实现月球软着陆及采样返回;若嫦娥五号的质量为m,在月球表面上受到的重力为P,月球的半径为R,则嫦娥五号在距月球表面高度为h的圆轨道上做匀速圆周运动时( )
| A. | 线速度的大小为R$\sqrt{\frac{P}{m(R+h)}}$ | B. | 周期为$\frac{2π}{R}$$\sqrt{\frac{m(R+h)}{P}}$ | ||
| C. | 动能为$\frac{P{R}^{2}}{2(R+h)}$ | D. | 所受月球的引力大小$\frac{P{R}^{2}}{(R+h)^{2}}$ |
5.下列说法中正确的是( )
| A. | 物体的温度升高时,其内部每个分子热的动能都一定增大 | |
| B. | 气体的压强越大,单位体积内气体的分子个数一定越多 | |
| C. | 物体的温度越高,其内部分子的平均动能就一定越大 | |
| D. | 分子间距离减小,分子间的引力和斥力都一定减小 |
15. 如图所示,两木块M、N从固定斜面顶端沿左边和右边同时由静止滑下,且两术块与斜面间的动摩擦因数相同,图中α+β=90°且α>β.则关于两物块沿斜面下滑过程的说法正确的是( )
如图所示,两木块M、N从固定斜面顶端沿左边和右边同时由静止滑下,且两术块与斜面间的动摩擦因数相同,图中α+β=90°且α>β.则关于两物块沿斜面下滑过程的说法正确的是( )
 如图所示,两木块M、N从固定斜面顶端沿左边和右边同时由静止滑下,且两术块与斜面间的动摩擦因数相同,图中α+β=90°且α>β.则关于两物块沿斜面下滑过程的说法正确的是( )
如图所示,两木块M、N从固定斜面顶端沿左边和右边同时由静止滑下,且两术块与斜面间的动摩擦因数相同,图中α+β=90°且α>β.则关于两物块沿斜面下滑过程的说法正确的是( )| A. | M的加速度比N的加速度大 | |
| B. | M在斜面上运动的时间更长 | |
| C. | M到达水平地面时的速度比N到达水平地面时的速度大 | |
| D. | M克服摩擦力所做的功必比N克服摩擦力所做的功小 |
2.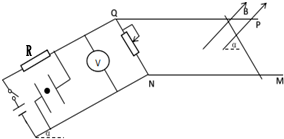 如图所示的电路固定在光滑绝缘斜面上,平行板电容器两极板垂直于斜面且与底边平行,定值电阻R,水平放置的平行金属导轨PQ、MN与电路相连,导体棒垂直于导轨放置且与导轨接触良好.在导轨间加一与水平面成α角斜向右上的匀强磁场,闭合开关,两板间的带电小球恰能静止.现把滑动变阻器滑动端向N端移动,导体棒始终静止不动,忽略周围电流对磁场的影响,下列说法正确的是( )
如图所示的电路固定在光滑绝缘斜面上,平行板电容器两极板垂直于斜面且与底边平行,定值电阻R,水平放置的平行金属导轨PQ、MN与电路相连,导体棒垂直于导轨放置且与导轨接触良好.在导轨间加一与水平面成α角斜向右上的匀强磁场,闭合开关,两板间的带电小球恰能静止.现把滑动变阻器滑动端向N端移动,导体棒始终静止不动,忽略周围电流对磁场的影响,下列说法正确的是( )
 如图所示的电路固定在光滑绝缘斜面上,平行板电容器两极板垂直于斜面且与底边平行,定值电阻R,水平放置的平行金属导轨PQ、MN与电路相连,导体棒垂直于导轨放置且与导轨接触良好.在导轨间加一与水平面成α角斜向右上的匀强磁场,闭合开关,两板间的带电小球恰能静止.现把滑动变阻器滑动端向N端移动,导体棒始终静止不动,忽略周围电流对磁场的影响,下列说法正确的是( )
如图所示的电路固定在光滑绝缘斜面上,平行板电容器两极板垂直于斜面且与底边平行,定值电阻R,水平放置的平行金属导轨PQ、MN与电路相连,导体棒垂直于导轨放置且与导轨接触良好.在导轨间加一与水平面成α角斜向右上的匀强磁场,闭合开关,两板间的带电小球恰能静止.现把滑动变阻器滑动端向N端移动,导体棒始终静止不动,忽略周围电流对磁场的影响,下列说法正确的是( )| A. | 带电小球沿斜面向上滑动 | |
| B. | R的电功率变小 | |
| C. | 伏特表示数变小 | |
| D. | 导体棒有向左运动的趋势,且对导轨的压力变大 |
19.现代生活中人类与电磁波结下了不解之缘,你认为下列陈述中哪些符合事实( )
| A. | 电磁波是电磁场由产生的区域向远处传播形成的 | |
| B. | 在真空中电磁波的传播速度小于真空中的光速 | |
| C. | 空间有变化的电场(或磁场)存在,一定能形成电磁波 | |
| D. | 把手机放在抽成真空的玻璃盒中,手机接收不到电磁波的信号,所以拨打该手机号码,手机不会响铃(或振动) |
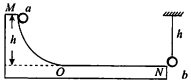 如图所示,固定的光滑轨道MON的ON段水平,且与MO段平滑连接.将质量为m,的小球a从M处由静止释放后沿MON运动,在N处与质量也为m的小球b发生正碰并粘在一起.已知MN两处的高度差为h,碰撞前小球b用长为k的轻绳悬挂于N处附近.两球均可视为质点,且碰撞时间极短.
如图所示,固定的光滑轨道MON的ON段水平,且与MO段平滑连接.将质量为m,的小球a从M处由静止释放后沿MON运动,在N处与质量也为m的小球b发生正碰并粘在一起.已知MN两处的高度差为h,碰撞前小球b用长为k的轻绳悬挂于N处附近.两球均可视为质点,且碰撞时间极短.