题目内容
5.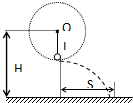 如图所示,用细线把小球悬挂在墙壁的钉子O上,小球绕悬点O在竖直平面内做圆周运动.小球质量为2kg,绳长L为0.8m,悬点距地面高度为1.6m.小球运动至最低点时,绳恰好被拉断,小球着地时速度与水平成45°,当地重力加速度为10m/s2.求:
如图所示,用细线把小球悬挂在墙壁的钉子O上,小球绕悬点O在竖直平面内做圆周运动.小球质量为2kg,绳长L为0.8m,悬点距地面高度为1.6m.小球运动至最低点时,绳恰好被拉断,小球着地时速度与水平成45°,当地重力加速度为10m/s2.求:(1)细线刚被拉断时,小球的速度多大?
(2)细线所能承受的最大拉力?
分析 (1)细线刚被拉断时,小球的速度即以后小球做平抛运动的初速度.而平抛运动运用运动的分解法研究:由下落的高度求出小球落地时竖直分速度,根据平行四边形定则求初速度.
(2)细线刚被拉断时所能承受的拉力最大,在最低点,由合力提供向心力,由牛顿第二定律求最大拉力.
解答 解:(1)细线被拉断后小球做平抛运动,竖直方向有 ${v}_{y}^{2}$=2g(H-L)
得 vy=$\sqrt{2g(H-L)}$=$\sqrt{2×10×(1.6-0.8)}$=4m/s
小球着地时速度与水平成45°,据平行四边形定则得:
v0=vy=4m/s
所以细线刚被拉断时,小球的速度为4m/s.
(2)在最低点,以小球为研究对象,根据牛顿第二定律得:
F-mg=m$\frac{{v}_{0}^{2}}{L}$
解得:F=m(g+$\frac{{v}_{0}^{2}}{L}$)=2×(10+$\frac{{4}^{2}}{0.8}$)N=60N.
答:
(1)细线刚被拉断时,小球的速度为4m/s.
(2)细线所能承受的最大拉力为60N.
点评 本题是圆周运动和平抛运动的综合运用,关键是要知道圆周运动向心力的来源,掌握平抛运动在水平方向和竖直方向上的运动规律.

练习册系列答案
相关题目
16.下列说法正确的是( )
| A. | 泊松亮斑是光的衍射现象,玻璃中的气泡看起来特别明亮是光的全反射现象 | |
| B. | 相对论认为空间和时间与物质的运动状态有关 | |
| C. | 交警通过发射超声波测量车速是利用了波的干涉原理 | |
| D. | 变化的磁场一定会产生变化的电场 | |
| E. | 在“用单摆测重力加速度”的实验中,测量n次全振动的总时间时,计时的起始位置应选在小球运动到最低点时为宜 |
14.下列关于电磁波的说法正确的是( )
| A. | 电场随时间变化时一定产生电磁波 | |
| B. | 常用的遥控器通过发出紫外线脉冲信号来遥控电视机 | |
| C. | 电磁波在真空中的传播速度与电磁波的频率无关 | |
| D. | 光在真空中运动的速度在不同惯性系中测得的数值可能不同 |
15. 如图所示,两木块M、N从固定斜面顶端沿左边和右边同时由静止滑下,且两术块与斜面间的动摩擦因数相同,图中α+β=90°且α>β.则关于两物块沿斜面下滑过程的说法正确的是( )
如图所示,两木块M、N从固定斜面顶端沿左边和右边同时由静止滑下,且两术块与斜面间的动摩擦因数相同,图中α+β=90°且α>β.则关于两物块沿斜面下滑过程的说法正确的是( )
 如图所示,两木块M、N从固定斜面顶端沿左边和右边同时由静止滑下,且两术块与斜面间的动摩擦因数相同,图中α+β=90°且α>β.则关于两物块沿斜面下滑过程的说法正确的是( )
如图所示,两木块M、N从固定斜面顶端沿左边和右边同时由静止滑下,且两术块与斜面间的动摩擦因数相同,图中α+β=90°且α>β.则关于两物块沿斜面下滑过程的说法正确的是( )| A. | M的加速度比N的加速度大 | |
| B. | M在斜面上运动的时间更长 | |
| C. | M到达水平地面时的速度比N到达水平地面时的速度大 | |
| D. | M克服摩擦力所做的功必比N克服摩擦力所做的功小 |
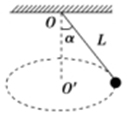 用细线悬吊着一个质量为m的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向夹角为α,线长为L,如图所示,小球受哪些力重力、拉力,小球的向心力大小为mgtanα.
用细线悬吊着一个质量为m的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向夹角为α,线长为L,如图所示,小球受哪些力重力、拉力,小球的向心力大小为mgtanα.