题目内容
1.某星球的质量为M,在该星球表面某一倾角为θ的山坡上(相当于是倾角为θ的斜面)以初速度v0平抛一物体,经过时间t该物体落到山坡上.(不计一切阻力,万有引力常数为G)求:(1)在该星球表面的重力加速度g
(2)欲使该物体不再落回该星球的表面,至少应以多大的速度抛出该物体?
分析 抓住平抛运动竖直位移和水平位移的关系,结合运动学公式求出星球表面的重力加速度.
根据万有引力等于重力求出星球的半径,结合重力提供向心力求出最小速度.
解答 解:(1)根据tanθ=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}$,
解得星球表面的重力加速度为:g=$\frac{2{v}_{0}tanθ}{t}$.
(2)根据mg=m$\frac{{v}^{2}}{R}$得:v=$\sqrt{gR}$,
又GM=gR2,解得:R=$\sqrt{\frac{GM}{g}}$,
则有:v=$\sqrt{\sqrt{GMg}}=(\frac{2GM{v}_{0}tanθ}{t})^{\frac{1}{4}}$.
答:在该星球表面的重力加速度为$\frac{2{v}_{0}tanθ}{t}$.
(2)欲使该物体不再落回该星球的表面,至少应以$(\frac{2GM{v}_{0}tanθ}{t})^{\frac{1}{4}}$的速度抛出该物体.
点评 本题考查了平抛运动与万有引力定律的综合,通过平抛运动的规律求出星球表面的重力加速度是关键,掌握万有引力提供向心力和万有引力等于重力这两个理论,并能灵活运用.

练习册系列答案
相关题目
11.在高速公路上发生一起交通事故,一辆质量为1500kg向南行驶的长途客车迎面撞上了一质量为3000kg向北行驶的卡车,碰后两车接在一起,并向南滑行了一小段距离后停止,根据测速仪的测定,长途客车碰前以20m/s的速率行驶,由此可判断卡车碰前的行驶速率( )
| A. | 大于10m/s | B. | 小于10m/s | ||
| C. | 大于20m/s小于30m/s | D. | 大于30m/s小于40m/s |
12.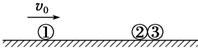 如图所示,在光滑的水平面上有三个完全相同的小球,它们排列成一条直线,2、3小球静止,并靠在一起,1小球以速度v0射向它们.假设碰撞过程中没有机械能损失,则碰后三个小球的速度可能是( )
如图所示,在光滑的水平面上有三个完全相同的小球,它们排列成一条直线,2、3小球静止,并靠在一起,1小球以速度v0射向它们.假设碰撞过程中没有机械能损失,则碰后三个小球的速度可能是( )
 如图所示,在光滑的水平面上有三个完全相同的小球,它们排列成一条直线,2、3小球静止,并靠在一起,1小球以速度v0射向它们.假设碰撞过程中没有机械能损失,则碰后三个小球的速度可能是( )
如图所示,在光滑的水平面上有三个完全相同的小球,它们排列成一条直线,2、3小球静止,并靠在一起,1小球以速度v0射向它们.假设碰撞过程中没有机械能损失,则碰后三个小球的速度可能是( )| A. | v1<v2<v3 | B. | v1=0,v2=v3=$\frac{1}{2}$v0 | C. | v1=v2=v3=$\frac{1}{3}$v0 | D. | v1=v2=0,v3=v0 |
9.竖直上抛一个物体,不计空气阻力,在上升过程与下落到出发点的两过程中( )
| A. | 经历的时间相等 | B. | 发生的位移相等 | ||
| C. | 重力对物体的冲量相同 | D. | 动量变化相等 |
16.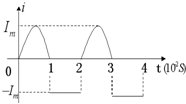 如图所示表示一交流电随时间而变化的图象,其中电流的正值为正弦曲线的正半周,其最大值为Im;电流的负值的强度为Im,则该交流电的有效值为( )
如图所示表示一交流电随时间而变化的图象,其中电流的正值为正弦曲线的正半周,其最大值为Im;电流的负值的强度为Im,则该交流电的有效值为( )
 如图所示表示一交流电随时间而变化的图象,其中电流的正值为正弦曲线的正半周,其最大值为Im;电流的负值的强度为Im,则该交流电的有效值为( )
如图所示表示一交流电随时间而变化的图象,其中电流的正值为正弦曲线的正半周,其最大值为Im;电流的负值的强度为Im,则该交流电的有效值为( )| A. | $\frac{{I}_{m}}{\sqrt{2}}$ | B. | $\sqrt{2}$Im | C. | Im | D. | $\frac{{\sqrt{3}}}{2}{I_m}$ |
6.关于胡克定律的下列说法,正确的是( )
| A. | 拉力相同、伸长不相同的弹簧,它们的劲度系数相同 | |
| B. | 劲度系数相同的弹簧,弹簧的伸长也一定相同 | |
| C. | 劲度系数相同的弹簧,弹簧的弹力也一定相同 | |
| D. | 劲度系数和拉力、伸长没有关系,它只决定于弹簧的材料、长度、弹簧丝的粗细 |
13.质量为1kg的物体在向上的拉力作用下由静止开始以2m/s2的加速度匀加速上升,在上升1秒的过程中有,( )
| A. | 合外力做功12J | B. | 重力做功10J | ||
| C. | 拉力做功12J | D. | 物体的机械能增加了2J |
10.关于日心说被人们接受的原因是( )
| A. | 太阳总是从东面升起,从西面落下 | |
| B. | 日心说符合宗教神学得观点 | |
| C. | 若以太阳为中心许多问题都可以解决,对行星的描述也变得简单 | |
| D. | 地球是围绕太阳运转的 |
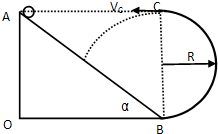 如图所示,光滑的斜面体OAB固定在水平地面上,在其右端B点与固定的光滑半圆形轨道平滑连接,半圆轨道与水平地面相切于B点,且半圆轨道的最高点C与斜面顶端A处于同一水平高度.小滑块(可看成质点)的质量为m,半圆轨道半径为R,斜面倾角α=45°(不计空气阻力和在B点处的能量损失).
如图所示,光滑的斜面体OAB固定在水平地面上,在其右端B点与固定的光滑半圆形轨道平滑连接,半圆轨道与水平地面相切于B点,且半圆轨道的最高点C与斜面顶端A处于同一水平高度.小滑块(可看成质点)的质量为m,半圆轨道半径为R,斜面倾角α=45°(不计空气阻力和在B点处的能量损失).