题目内容
12.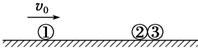 如图所示,在光滑的水平面上有三个完全相同的小球,它们排列成一条直线,2、3小球静止,并靠在一起,1小球以速度v0射向它们.假设碰撞过程中没有机械能损失,则碰后三个小球的速度可能是( )
如图所示,在光滑的水平面上有三个完全相同的小球,它们排列成一条直线,2、3小球静止,并靠在一起,1小球以速度v0射向它们.假设碰撞过程中没有机械能损失,则碰后三个小球的速度可能是( )| A. | v1<v2<v3 | B. | v1=0,v2=v3=$\frac{1}{2}$v0 | C. | v1=v2=v3=$\frac{1}{3}$v0 | D. | v1=v2=0,v3=v0 |
分析 碰撞中系统动量守恒列出等式.碰撞中不损失机械能,根据机械能守恒列式求解.
解答 解:2、3小球静止,并靠在一起,1球以速度v0射向它们,碰撞前系统动量为mv0,碰撞中系统动量守恒,机械能守恒,
A、如果v1<v2<v3,只要满足统动量守恒,机械能守恒即可,所以碰后三个小球的速度可能为v1<v2<v3,故A正确;
B、如果v1=0,v2=v3=$\frac{1}{2}$v0,碰撞后系统动量为mv0,碰撞后的总动能为:$\frac{1}{4}$mv02,机械能不守恒,不符合题意,故B错误.
C、如果v1=0 v2=v3=$\frac{{v}_{0}}{3}$,碰撞后系统总动量为$\frac{2}{3}$mv0,碰撞过程不守恒,不符合题意,故C错误.
D、球的碰撞过程为:由于球1与球2发生碰撞时间极短,球2的位置来不及发生变化,这样球2对球3也就无法产生力的作用,即球3不会参与此次碰撞过程.而球1与球2发生的是弹性碰撞,质量又相等,故它们在碰撞中实现速度交换,碰后球1立即停止,球2速度立即变为v0;此后球2与球3碰撞,再一次实现速度交换.所以碰后球1、球2的速度为零,球3速度为v0.故D正确.
故选:AD
点评 本题考查了求碰撞后球的速度,知道碰撞过程动量守恒、机械能守恒,应用动量守恒定律和机械能守恒定律即可正确解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列叙述中正确的是( )
| A. | 布朗运动就是液体分子的无规则运动 | |
| B. | 当分子力表现为引力时,分子势能随分子间距离的增加而增加 | |
| C. | 对于一定质量的理想气体,温度升高时,压强可能减小 | |
| D. | 已知水的密度和水的摩尔质量,则可以计算出阿伏加德罗常数 | |
| E. | 扩散现象说明分子之间存在空隙,同时分子在永不停息地做无规则运动 |
3.某著名极限运动员在美国新墨西哥州上空,从距地面高度约3.9万米的氦气球携带的太空舱上跳下,在最后几千英尺打开降落伞,并成功着陆.假设降落伞在最后的匀速竖直下降过程中遇到水平方向吹来的风,若风速越大,则降落伞( )
| A. | 下落的时间越短 | B. | 下落的时间越长 | C. | 落地时速度越小 | D. | 落地时速度越大 |
4.交流发电机在工作时的电动势e=EmSinωt.若将线圈匝数,线圈面积和角速度ω都提高到原来的两倍,其他条件不变,则电动势变为( )
| A. | e=8EmSinωt | B. | e=8EmSin2ωt | C. | e=4EmSin2ωt | D. | e=4EmSinωt |
2.下列说法符合史实的是( )
| A. | 第谷在行星观测数据基础上发现了行星的运动规律 | |
| B. | 牛顿发现了万有引力定律并给出了万有引力常量的数值 | |
| C. | 卡文迪许首次在实验室里测出了万有引力常量 | |
| D. | 牛顿应用万有引力定律发现了海王星 |
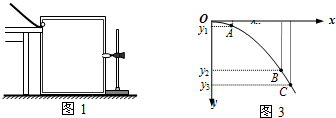
 如图为火车站装载货物的原理示意图,设AB段是距水平传送带装置高为H=5m的光滑斜面,水平段BC使用水平传送带装置,BC长L=8m,与货物包的摩擦系数为μ=0.6,皮带轮的半径为R=0.2m,上部距车厢底水平面的高度h=0.45m.设货物由静止开始从A点下滑,经过B点时速度大小为10m/s.通过调整皮带轮(不打滑)的转动角速度ω可使货物经C点抛出后落在车厢上的不同位置,取g=10m/s2,求:
如图为火车站装载货物的原理示意图,设AB段是距水平传送带装置高为H=5m的光滑斜面,水平段BC使用水平传送带装置,BC长L=8m,与货物包的摩擦系数为μ=0.6,皮带轮的半径为R=0.2m,上部距车厢底水平面的高度h=0.45m.设货物由静止开始从A点下滑,经过B点时速度大小为10m/s.通过调整皮带轮(不打滑)的转动角速度ω可使货物经C点抛出后落在车厢上的不同位置,取g=10m/s2,求: