题目内容
如图所示,弹簧下面挂一质量为m的物体,物体在竖直方向上作振幅为A的简谐运动,当物体振动到最高点时,弹簧正好为原长,弹簧在弹性限度内,则物体在振动过程中
| A.物体在最低点时的弹力大小应为mg |
| B.弹簧的弹性势能和物体动能总和不变 |
| C.弹簧的最大弹性势能等于2mgA |
| D.物体的最大动能应等于mgA |
C
解析试题分析:据题意,物体的平衡位置在弹力F和重力G相等的位置,该位置合力为0 ,由于物体的振幅为A,则物体向上只能振动到平衡位置上方距离平衡位置为A的地方,该位置合力为G方向向下;据简谐振动的对称性,向下振动只能振动到距离平衡位置下方距离平衡位置为A的位置,此位置的合力也为G方向向上;如图所示: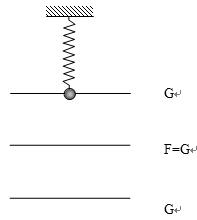
所以物体在最低点时的弹力为F-G=G,即弹力F=2G,则A选项错误;由于物体只受到重力和弹力,所以整个系统(球和弹簧)机械能守恒,即物体的动能、重力势能和弹簧的弹性势能之和不变,所以B选项错误;当物体处于最低点时,弹性势能最大,从最高点到最低点,据动能定理有:WG-W弹=0,即弹性势能与重力势能变化相等,所以弹性势能变化为E=2mgA,所以C选项正确;物体的最大动能出现在平衡位置,从最高点到此平衡位置据机械能守恒定律有:E总=E弹+EP+EK,而EP=mgA,由于K(2A)2/2=2mgA则E弹=KA2/2=mgA/2,所以EK=mgA/2,D选项错误。
考点:本题考查对机械能守恒定律的理解和简谐运动的理解。

质量相同的两个小球,分别用长为L和2L的细绳悬挂在天花板上,如图所示,分别拉起小球使线伸直呈水平状态,然后轻轻释放,当小球到达最低位置时 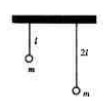
| A.两球运动的线速度相等 |
| B.两球运动的角速度相等 |
| C.两球运动的加速度均为3g |
| D.细绳对两球的拉力均为3mg |
半径为r和R(r<R)的光滑半圆形槽,其圆心均在同一水平面上,如图所示,质量相等的两物体(可看成质点)分别自半圆形槽左边缘的最高点无初速地释放,在下滑过程中关于两物体的说法,不正确的是 
| A.机械能均逐渐减小 |
| B.经最低点时动能相等 |
| C.两球在最低点加速度大小不等 |
| D.机械能总是相等的 |
如图所示,小球从高处下落到竖直放置的轻弹簧上,那么小球从接触弹簧开始到将弹簧压缩到最短的过程中(弹簧保持竖直),下列关于能的叙述正确的是 
| A.弹簧的弹性势能不断增大 |
| B.小球的动能先增大后减小 |
| C.小球的重力势能先增大后减小 |
| D.小球的机械能总和先增大后减小 |
如右图所示,一轻绳通过无摩擦的小定滑轮O与小球B连接,另一端与套在光滑竖直杆上的小物块A连接,杆两端固定且足够长,物块A由静止从图示位置释放后,先沿杆向上运动. 设某时刻物块A运动的速度大小为vA,小球B运动的速度大小为vB,轻绳与杆的夹角为θ,则
| A.vA=vBcosθ |
| B.vB=vAcosθ |
| C.小球B减小的势能等于物块A增加的动能 |
| D.当物块A上升到与滑轮等高时,它的机械能最大 |







