题目内容
9．
如图，质量分别为3m、2m、m的三个小球A、B、C用两根长为L的轻绳相连，置于倾角为30°、高为L的固定斜面上，A球恰好能从斜面顶端外落下，弧形挡板使小球能顺利地由斜向上运动转为竖直向下运动且无机械能损失，小球落地后不再弹起，则静止起释放它们，不计所有摩擦，求C球落到地面时的速度大小．
分析 在A球未落地前，A、B、C组成的系统机械能守恒，列式可求得A球刚要落地时的速度大小．在A球落地后，B球未落地前，B、C组成的系统机械能守恒，在B球落地后，C球未落地前，C球在下落过程中机械能守恒，分两个过程由机械能守恒列式可求得C球刚要落地时的速度大小．
解答 解：设A球刚要落地时速度大小为v1
由机械能守恒定律：3mgL-3mgL•sin30°=$\frac{1}{2}$×6m•v12
则v1=$\sqrt{\frac{gL}{2}}$
设B球刚要落地时速度为v2，C球刚要落地时速度为v3
由机械能守恒定律：2mgL-mgL•sin30°=$\frac{1}{2}$×3mv22-$\frac{1}{2}$×3mv12
则v2=$\sqrt{\frac{3}{2}gL}$
mgL=$\frac{1}{2}$mv32-$\frac{1}{2}$mv22
则v3=$\sqrt{\frac{7}{2}gL}$
答：C球刚要落地时的速度大小为$\sqrt{\frac{7}{2}gL}$．
点评 本题绳系系统机械能守恒问题，关键要善于选择研究的过程，分段进行列式求解．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
半径为R的水平圆盘，绕通过圆心的竖直轴匀速转动，A为圆盘边缘上的一点，在O的正上方有一个可以视为质点的小球，以初速度υ水平抛出时，半径OA方向恰与υ的方向相同，如图所示．若小球与圆盘只碰一次，且正好落在A点，则小球抛出时距离O点的高度h=$\frac{g{R}^{2}}{2{v}^{2}}$，圆盘转动的角速度大小$\frac{2nπv}{R}$，（n=1，2，3，…）．（重力加速度为g）
如图甲所示，相距很近竖直放置的平行板电容器，A、B两极板中心各开有一小孔，靠近A极板小孔有一处电子枪F，电子枪能够持续均匀地向A、B极板内发射出初速度为v0电子，电子的质量为m、电量为e．在A、B两板之间加上图乙所示的交变电压，其中0＜k＜1，U0=$\frac{m{{v}_{0}}^{2}}{6e}$；t=0时A板电势高于B板电势．紧靠B板水平放置的C、D极板间的电场电压也等于U0，板长为L，两板间距为d，距C、D极板右端$\frac{L}{2}$处垂直放置很大的荧光屏PQ．不计电子的重力和它们之间的相互作用，电子在电容器AB中的运动时间可以忽略不计．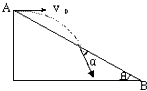
从倾角为θ的足够长的斜面上的A点，先后将同一小球以不同的初速度水平向右抛出．第一次初速度为v1，球落到斜面上的瞬时速度方向与斜面夹角为α1，第二次初速度为v2，球落到斜面上的瞬时速度方向与斜面夹角为α2，若v1＞v2，则（ ）
如图所示，小球C在光滑的水平直轨道上处于静止状态．在它右边有两个小球A和B用轻质弹簧相连，以相同的速度v0向C球运动，C与B发生碰撞并立即结成一个整体D．试判断在这之后小球A能否向右运动．已知A、B、C三球的质量均为m．
如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图，已知波的传播速度v=2m/s．试回答．
如图所示在光滑的水平地面上静止放置一辆，上表面光滑右端固定一个半径为R光滑的四分之一圆弧的小车，小车的质量为2m（包括圆弧轨道），质量为m的物体以v0沿水平方向向右运动冲上小车，在之后的运动过程中物体能从轨道上端飞出，