题目内容
6. 半径为R的水平圆盘,绕通过圆心的竖直轴匀速转动,A为圆盘边缘上的一点,在O的正上方有一个可以视为质点的小球,以初速度υ水平抛出时,半径OA方向恰与υ的方向相同,如图所示.若小球与圆盘只碰一次,且正好落在A点,则小球抛出时距离O点的高度h=$\frac{g{R}^{2}}{2{v}^{2}}$,圆盘转动的角速度大小$\frac{2nπv}{R}$,(n=1,2,3,…).(重力加速度为g)
半径为R的水平圆盘,绕通过圆心的竖直轴匀速转动,A为圆盘边缘上的一点,在O的正上方有一个可以视为质点的小球,以初速度υ水平抛出时,半径OA方向恰与υ的方向相同,如图所示.若小球与圆盘只碰一次,且正好落在A点,则小球抛出时距离O点的高度h=$\frac{g{R}^{2}}{2{v}^{2}}$,圆盘转动的角速度大小$\frac{2nπv}{R}$,(n=1,2,3,…).(重力加速度为g)
分析 小球做平抛运动,根据水平位移和初速度求出平抛运动的时间,根据时间求出高度h.抓住平抛运动的时间和圆周运动的时间相等,求出圆盘转动的角速度.
解答 解:平抛运动的时间t=$\frac{R}{v}$,
则高度h=$\frac{1}{2}g{t}^{2}=\frac{1}{2}g×\frac{{R}^{2}}{{v}^{2}}=\frac{g{R}^{2}}{2{v}^{2}}$.
根据圆周运动的周期性,结合时间相等有:$\frac{R}{v}=n\frac{2π}{ω}$,
解得$ω=\frac{2nπv}{R}$,(n=1,2,3,…)
故答案为:$\frac{g{R}^{2}}{2{v}^{2}}$,$\frac{2nπv}{R}$,(n=1,2,3,…)
点评 本题考查了平抛运动和圆周运动的基本运用,知道平抛运动在水平方向和竖直方向上的运动规律,运用运动学公式灵活求解.本题需注意圆周运动的周期性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17. 如图所示,将一不带电的绝缘枕形导体P放在正点电荷Q的电场中,导体P的a、b两端分别带上了感应负电荷与等量的感应正电荷,另外,导体内部还有两点c、d,则以下说法错误的是( )
如图所示,将一不带电的绝缘枕形导体P放在正点电荷Q的电场中,导体P的a、b两端分别带上了感应负电荷与等量的感应正电荷,另外,导体内部还有两点c、d,则以下说法错误的是( )
 如图所示,将一不带电的绝缘枕形导体P放在正点电荷Q的电场中,导体P的a、b两端分别带上了感应负电荷与等量的感应正电荷,另外,导体内部还有两点c、d,则以下说法错误的是( )
如图所示,将一不带电的绝缘枕形导体P放在正点电荷Q的电场中,导体P的a、b两端分别带上了感应负电荷与等量的感应正电荷,另外,导体内部还有两点c、d,则以下说法错误的是( )| A. | 导体上a、b两端的电势高低关系是φa=φb | |
| B. | 导体上a、b两端的电势高低关系是φa>φb | |
| C. | 导体内部c、d两点的场强大小关系是Ec=Ed=0 | |
| D. | 感应电荷在导体内部c、d两点产生的场强大小关系是Ec>Ed≠0 |
14. 点电荷M、N、P、Q的带电量相等,M、N带正电,P、Q带负电,它们分别处在一个矩形的四个顶点上,O为矩形的中心.它们产生静电场的等势面如图中虚线所示,电场中a、b、c、d四个点与MNPQ共面,则下列说法正确的是( )
点电荷M、N、P、Q的带电量相等,M、N带正电,P、Q带负电,它们分别处在一个矩形的四个顶点上,O为矩形的中心.它们产生静电场的等势面如图中虚线所示,电场中a、b、c、d四个点与MNPQ共面,则下列说法正确的是( )
 点电荷M、N、P、Q的带电量相等,M、N带正电,P、Q带负电,它们分别处在一个矩形的四个顶点上,O为矩形的中心.它们产生静电场的等势面如图中虚线所示,电场中a、b、c、d四个点与MNPQ共面,则下列说法正确的是( )
点电荷M、N、P、Q的带电量相等,M、N带正电,P、Q带负电,它们分别处在一个矩形的四个顶点上,O为矩形的中心.它们产生静电场的等势面如图中虚线所示,电场中a、b、c、d四个点与MNPQ共面,则下列说法正确的是( )| A. | 如取无穷远处电势为零,则O点电势为零,场强不为零 | |
| B. | O、b两点电势φb>φO,O、b两点场强Eb<EO | |
| C. | 将某一正试探电荷从b点沿直线移动到c点,电场力一直做正功 | |
| D. | 某一负试探电荷在各点的电势能大小关系为?a<?b<?O<?d<?c |
1.如图所示,A、B是某“门”电路的输入信号,Z是相应的输出信号.由此可以判断,该门电路是( )


| A. | “或”门 | B. | “与”门 | C. | “非”门 | D. | “与非”门 |
11. 如图所示,一圆形闭合小铜环从高处由静止开始下落,穿过一根竖直悬挂的、质量为m的条形磁铁,铜环的中心轴线与条形磁铁的中心轴线始终保持重合.则细绳中弹力F随时间t的变化关系图象可能是( )
如图所示,一圆形闭合小铜环从高处由静止开始下落,穿过一根竖直悬挂的、质量为m的条形磁铁,铜环的中心轴线与条形磁铁的中心轴线始终保持重合.则细绳中弹力F随时间t的变化关系图象可能是( )
 如图所示,一圆形闭合小铜环从高处由静止开始下落,穿过一根竖直悬挂的、质量为m的条形磁铁,铜环的中心轴线与条形磁铁的中心轴线始终保持重合.则细绳中弹力F随时间t的变化关系图象可能是( )
如图所示,一圆形闭合小铜环从高处由静止开始下落,穿过一根竖直悬挂的、质量为m的条形磁铁,铜环的中心轴线与条形磁铁的中心轴线始终保持重合.则细绳中弹力F随时间t的变化关系图象可能是( )| A. |  | B. | 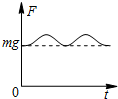 | C. |  | D. | 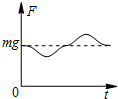 |
18. 如图所示,两个闭合正方形线框A、B的中心重合,放在同一水平面内.当小线框A中通有不断增大的顺时针方向的电流时,对于线框B,下列说法中正确的是( )
如图所示,两个闭合正方形线框A、B的中心重合,放在同一水平面内.当小线框A中通有不断增大的顺时针方向的电流时,对于线框B,下列说法中正确的是( )
 如图所示,两个闭合正方形线框A、B的中心重合,放在同一水平面内.当小线框A中通有不断增大的顺时针方向的电流时,对于线框B,下列说法中正确的是( )
如图所示,两个闭合正方形线框A、B的中心重合,放在同一水平面内.当小线框A中通有不断增大的顺时针方向的电流时,对于线框B,下列说法中正确的是( )| A. | 有顺时针方向的电流且有收缩的趋势 | |
| B. | 有顺时针方向的电流且有扩张的趋势 | |
| C. | 有逆时针方向的电流且有收缩的趋势 | |
| D. | 有逆时针方向的电流且有扩张的趋势 |

 如图,质量分别为3m、2m、m的三个小球A、B、C用两根长为L的轻绳相连,置于倾角为30°、高为L的固定斜面上,A球恰好能从斜面顶端外落下,弧形挡板使小球能顺利地由斜向上运动转为竖直向下运动且无机械能损失,小球落地后不再弹起,则静止起释放它们,不计所有摩擦,求C球落到地面时的速度大小.
如图,质量分别为3m、2m、m的三个小球A、B、C用两根长为L的轻绳相连,置于倾角为30°、高为L的固定斜面上,A球恰好能从斜面顶端外落下,弧形挡板使小球能顺利地由斜向上运动转为竖直向下运动且无机械能损失,小球落地后不再弹起,则静止起释放它们,不计所有摩擦,求C球落到地面时的速度大小.