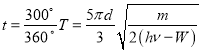题目内容
【题目】光电倍增管可将光信号转化为电信号并逐级放大，其前两个平行倍增极结构如图。当频率为
的入射光照射到第1倍增极的上表面MN时，极板上表面逸出大量速率不同、沿各个方向运动的光电子，空间加上垂直纸面的匀强磁场，可使从MN逸出的部分光电子打到第2倍增极的上表面PQ。已知第1倍增极金属的逸出功为W，两个倍增极长度均为d，水平间距为
，竖直间距为
，光电子电量为e、质量为m，普朗克常量为h，仅考虑光电子在纸面内运动且只受洛伦兹力作用。
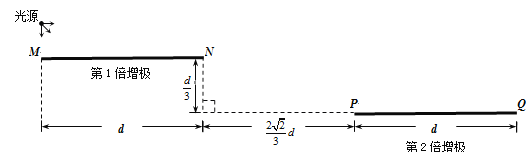
（1）求从MN上逸出的光电子的最大速率。
（2）若以最大速率、方向垂直MN逸出的光电子可以全部到达PQ，求磁感应强度的大小和方向。
（3）若保持（2）中的磁场不变，关闭光源后，发现仍有光电子持续击中PQ，求关闭光源后光电子持续击中PQ的时间。
【答案】（1）
（2）
，垂直纸面向内 （3）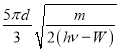
【解析】（1）由题可知入射光照射到第1倍增极上表面时发生光电效应
由爱因斯坦光电效应方程
解得：逸出的光电子的最大速率
（2）作出粒子在磁场中的运动轨迹图如图所示：
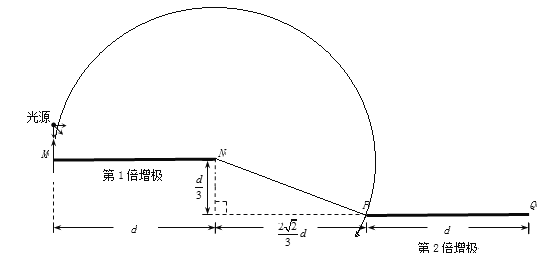
由图可知，从M点垂直向上射出的光电子经过磁场偏转恰好到达P点，圆心在N点
由几何关系得：偏转半径r=d
由牛顿第二定律得： 
解得： 
因光电子带负电，由偏转图象可知光电子向右偏转，由左手定则可知磁场方向为垂直纸面向内
（3）由于关闭光源前已有大量光电子在持续前往第2倍增极的路上，所以关闭光源后的一段时间，仍有光电子击中第2倍增极，因此“关闭光源后光电子持续击中PQ的时间”对应的是光电子从MN到达PQ的最长时间，最长时间对应的是轨迹圆心角最大的情况：当速率为最大时，对应的圆轨迹与PQ相切时圆心角最大；作出相应的运动轨迹如图所示：
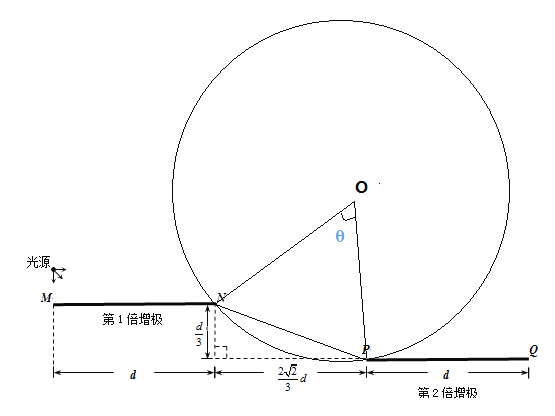
由图可知，当最大速度对应的轨迹圆不能与PQ相切，故从N端以最大速率逸出并击中P端的光电子的圆弧轨迹圆心角最大，所对应的时间最长，因为OP=ON=r=d=NP，故
是等边三角形，则
则光电子运动轨迹的圆心角为
，运动的周期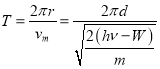
故运动的最长时间为
