题目内容
【题目】如图所示，水平轨道AB和CD与竖直圆轨道平滑相接于最低点，圆轨道在最低点稍微里外错开一点，外面是B点，里面是C点。整个轨道除AB部分粗糙外，其余部分均光滑，AB长度为S=10m。在CD部分的右侧有一与CD等高的传送带紧靠D点，并顺时针转动。质量为m2=1kg的乙物体静止在B点，质量为m1=0.5kg的物体甲从A点在恒定的拉力F=5N的作用下由静止开始向右运动，F与水平方向夹角为θ=37°，物体甲与AB间的动摩擦因数为μ1=0.2，物体运动到B点时撤去拉力，随后甲、乙发生正碰，碰后甲物体静止，乙物体滑上圆轨道，圆轨道的半径为R=0.5m，g=10m/s2，取sin37°=0.6，A、B可视为质点，求：
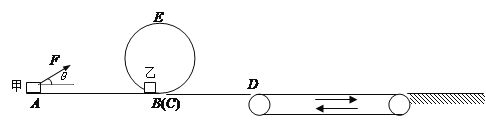
(1)物体乙运动到圆轨道最高点E时对轨道的压力为多大？
(2)传送带顺时针转动的转速可随意调节，使得物体乙离开传送带时速度随之变化。物体乙与传送带间的动摩擦因数为μ2=0.3，传送带的长度为L=3m，则物体滑离传送带的速度在什么范围内？
【答案】（1）22N； （2）
m/s≤v≤
m/s
【解析】试题分析：对物体受力分析，根据平衡条件和动能定理求出到达B点的速度，物体甲和乙碰撞过程动量守恒和机械能守恒联立解得到达E点的速度，再根据牛顿第二定律求出压力；若传送带速度足够小，则物体一直减速滑过，此时滑离传送带具有最小速度，由动能定理求出最小速度，若传送带速度足够大，物体一直加速滑过，此时滑离传送带具有最大速度，由动能定理求出最大速度，从而求出范围。
(1)从A到B过程中，物体受力分析如图所示：
根据平衡条件可得：
解得：FN1=2N
摩擦力为：
=0.4N
由动能定理得：
解得：v0=12m/s
物体甲和乙碰撞过程动量守恒，有：m1v0=m2v1
解得：v1=6m/s
物体乙在光滑轨道上运动过程中机械能守恒，则从B到E的过程中，由机械能守恒定律得：
解得：v2=4m/s
根据牛顿第二定律：
解得：FN2=22N
由牛顿第三定律得乙到圆轨道最高点E时对轨道的压力大小F 2'=22N
(2)①若传送带速度足够小，则物体一直减速滑过，此时滑离传送带具有最小速度，由动能定理得：
其中：
FN3=m2g
解得：
m/s
②若传送带速度足够大，物体一直加速滑过，此时滑离传送带具有最大速度，由动能定理得：
解得：
m/s
综上所述，物体滑离传送带的速度应有：m/s≤v≤m/s
