��Ŀ����
12��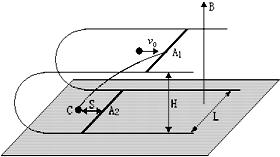 ��ͼ��ʾ���ڴŸ�Ӧǿ�ȴ�СΪB������ֱ���ϵ���ǿ�ų��У���һ�ϡ����������ˮƽ��ƽ�еġ�U���⻬�������죬�ڵ������ϸ���һ����ȫ��ͬ������Ϊm�����ʽ�����A1��A2����ʼʱ����������λ��ͬһ��ֱ�����Ҹ�������ֱ���������������ΪH�������ΪL�������㹻���ҵ��費�ƣ������˵�λ���ȵĵ���Ϊr������һ����Ϊ$\frac{m}{2}$�IJ�����С����ˮƽ���ҵ��ٶ�v0ײ����A1���е㣬ײ����С���䵽�²����ϵ�C�㣮C�����A2��ʼλ�����ΪS����
��ͼ��ʾ���ڴŸ�Ӧǿ�ȴ�СΪB������ֱ���ϵ���ǿ�ų��У���һ�ϡ����������ˮƽ��ƽ�еġ�U���⻬�������죬�ڵ������ϸ���һ����ȫ��ͬ������Ϊm�����ʽ�����A1��A2����ʼʱ����������λ��ͬһ��ֱ�����Ҹ�������ֱ���������������ΪH�������ΪL�������㹻���ҵ��費�ƣ������˵�λ���ȵĵ���Ϊr������һ����Ϊ$\frac{m}{2}$�IJ�����С����ˮƽ���ҵ��ٶ�v0ײ����A1���е㣬ײ����С���䵽�²����ϵ�C�㣮C�����A2��ʼλ�����ΪS������1����·�ڸ�Ӧ���������ֵ��
��2�������˶������и�Ӧ�����������˶���������
��3������A2���A1���ٶȱ�Ϊ1��3ʱ��A2�ܵ��İ�������С��
���� ��1��С��ײ�������˵Ĺ��̣����ض����غ㶨�ɣ����ݶ����غ㶨����ʽ������ƽ���˶��Ĺ����������С����ٶȣ��Ӷ���������˻�õ��ٶȣ����ɷ����ڶ��ɺ�ŷķ���ɽ���������˲���·�еĵ���������·�ڸ�Ӧ���������ֵ��
��2�������ڰ����������£�������A1�������˶���������A2�������˶����������ٶȴ�С���ʱ����·�ڸ�Ӧ����Ϊ0�����ݶ����غ㶨�ɺ������غ㶨�ɽ�����������
��3��������A1��A2������ͬһ������U�ε����϶��������˶����˶�������ͬ�������ң���ͬһʱ�����˶��и�Ÿ��߲�����Ӧ�綯�ƣ�������Ӧ�綯���ڿռ��еķ�����ͬ�������⣩����������Ӧ�綯���ڻ�·�еķ����෴�������ܵ綯�����������綯��֮���E=BL��v1-v2���������ǵ�����$I=\frac{{BL��{v_1}-{v_2}��}}{R}$������Ϊ������A1�и�Ӧ�����ķ�����ΪA1��A2�����ĸ�Ӧ�綯�ƴ�������$F=\frac{{{B^2}{L^2}��{v_1}-{v_2}��}}{R}$�������ٶȷ����෴�����������ݰ�������ʽ��⣮
��� �⣺��1����ײ����С�����ٶ�Ϊv1��������A1���ٶ�Ϊv01��ȡˮƽ����Ϊ�������ݶ����غ㶨�ɣ��� $\frac{m}{2}{v_0}=\frac{m}{2}��-{v_1}��+m{v_{01}}$����
����С���ƽ���˶�������ƽ���˶��ķֽ⣬�� S=v1t��$H=\frac{1}{2}g{t^2}$
��������ʽ��� v1=$S\sqrt{\frac{g}{2H}}$ ��
�ڴ���ٵ� ${v_{01}}=\frac{1}{2}��{v_0}+S\sqrt{\frac{g}{2H}}��$ ��
��·�ڸ�Ӧ�綯�Ƶ����ֵΪEm=BLv01
����ΪR=2Lr
���Ի�·�ڸ�Ӧ���������ֵΪ Im=$\frac{{B��{v_0}+s\sqrt{\frac{g}{2H}}��}}{4r}$�� ��
��2����Ϊ�ڰ������������£�������A1�������˶���������A2�������˶����������ٶȴ�С���ʱ����·�ڸ�Ӧ����Ϊ0�����������غ㶨�ɣ�$\frac{1}{2}mv_{01}^2=Q+\frac{1}{2}•2m{v^2}$ ��
����v�������ٶȴ�С���ʱ���ٶȣ����ݶ����غ㶨�ɣ�mv01=2mv
���� $v=\frac{1}{2}{v_{01}}$�������ʽ�� Q=$\frac{1}{16}m$${��{v_0}+s\sqrt{\frac{g}{2H}}��^2}$��
��3���������A1��A2�ٶȴ�С�ֱ�Ϊv1��v2�����ݶ����غ㶨�ɣ�mv01=mv1+mv2����$\frac{v_1}{v_2}=\frac{3}{1}$������${v_1}=\frac{3}{4}{v_{01}}$��${v_2}=\frac{1}{4}{v_{01}}$��
������A1��A2�ٶȷ������ң��������ֶ����ж�֪A1��A2�����ĸ�Ӧ�綯���ڻ�·�з����෴
���Ը�Ӧ�綯��ΪE=BL��v1-v2��������Ϊ$I=\frac{E}{2Lr}$��������ΪF=BIL������ A2�ܵ��İ�������СΪF=$\frac{{{B^2}L}}{8r}$$��{v_0}+s\sqrt{\frac{g}{2H}}��$��
��ȻA1�ܵ��İ�������СҲ��ˣ�ֻ���������෴��
��
��1����·�ڸ�Ӧ���������ֵ��$\frac{{B��{v_0}+s\sqrt{\frac{g}{2H}}��}}{4r}$��
��2�������˶������и�Ӧ������������������$\frac{1}{16}m$${��{v_0}+s\sqrt{\frac{g}{2H}}��^2}$��
��3��A2�ܵ��İ�������С��$\frac{{{B^2}L}}{8r}$$��{v_0}+s\sqrt{\frac{g}{2H}}��$��
���� ����Ҫע�ؽ�����A1��A2���˵��˶����̷��������ͬһʱ�����˶��и�Ÿ��߲�����Ӧ�綯��ʱ������������Ӧ�綯���ڻ�·�еķ���������·���ܵĸ�Ӧ�綯�ƣ�

 ��ͼ��ʾ��Ϊ�����Q�ĵ糡��A��B�ǵ糡�е����㣬������Ϊq=5��10-8���ص������ɣ���̽��ɣ�����A�㣬���ܵ糡��Ϊ2��10-3ţ���������ж���ȷ���ǣ�������
��ͼ��ʾ��Ϊ�����Q�ĵ糡��A��B�ǵ糡�е����㣬������Ϊq=5��10-8���ص������ɣ���̽��ɣ�����A�㣬���ܵ糡��Ϊ2��10-3ţ���������ж���ȷ���ǣ�������| A�� | ������q��A�����ߣ���õ�ĵ糡ǿ��Ϊ�� | |
| B�� | ������Ϊq�ĸ����ɷ���A�㣬A�㳡ǿ��СΪ4.0��104N/C������ָ��B | |
| C�� | B�㴦�ĵ糡ǿ��С��4.0��104N/C | |
| D�� | ������Ϊ2q�������ɷ���A�㣬A�㳡ǿ��СΪ8.0��104 N/C������ָ��B |
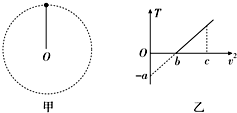
| A�� | ��������Ϊ$\frac{am}{b}$ | |
| B�� | ���ص��������ٶ�Ϊ$\frac{a}{m}$ | |
| C�� | ��v2=cʱ����������������СΪ$\frac{ac}{b}$+a | |
| D�� | ֻҪv2��b��С������͵����ߵ�ʱ�����������Ϊ6a |
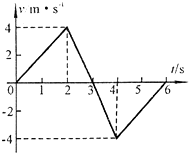 ij������һֱ���˶�����v-tͼ����ͼ��ʾ�����1s�������˶��ļ��ٶȴ�СΪ2m/s2���������ٶȷ�����ͬ������ͬ���෴������3s�������˶��ļ��ٶȴ�СΪ4m/s2���������ٶȷ����෴������ͬ���෴������4s�������˶��ļ��ٶȴ�СΪ4m/s2���������ٶȷ�����ͬ������ͬ���෴��ǰ3s�ڵ�λ��6m��ǰ6s�ڵ�λ��0m��
ij������һֱ���˶�����v-tͼ����ͼ��ʾ�����1s�������˶��ļ��ٶȴ�СΪ2m/s2���������ٶȷ�����ͬ������ͬ���෴������3s�������˶��ļ��ٶȴ�СΪ4m/s2���������ٶȷ����෴������ͬ���෴������4s�������˶��ļ��ٶȴ�СΪ4m/s2���������ٶȷ�����ͬ������ͬ���෴��ǰ3s�ڵ�λ��6m��ǰ6s�ڵ�λ��0m��