题目内容
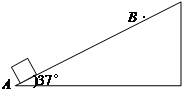
如图所示的装置中,轻绳将A、B相连,B置于光滑水平面上,人用拉力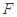 使B以
使B以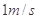 匀速的由P运动到Q,P、Q处绳与竖直方向的夹角分别为α1=37°,α2=53°.滑轮离光滑水平面高度
匀速的由P运动到Q,P、Q处绳与竖直方向的夹角分别为α1=37°,α2=53°.滑轮离光滑水平面高度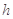 =2.4m,已知
=2.4m,已知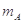 =10
=10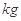 ,
,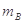 =20
=20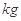 ,不计滑轮质量和摩擦,求在此过程中拉力F做的功(取sin37°=0.6,sin53°=0.8.
,不计滑轮质量和摩擦,求在此过程中拉力F做的功(取sin37°=0.6,sin53°=0.8.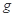 取
取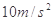 )
)
101.4J
解析试题分析:A的速度等于绳子收缩的速度,则由运动的合成与分解可得:物体在P点时,A上升的速度V1=vsinα1=0.6m/s;物体拉到Q点时,A上升的速度V1′=vsinα2=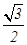 m/s;由几何关系可知,物体A上升的高度h′=
m/s;由几何关系可知,物体A上升的高度h′=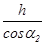 -
-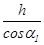 =1.5m由动能定理可得:WF-mgh′=
=1.5m由动能定理可得:WF-mgh′= mv12;
mv12;
解得:WF=mAgh′+ mAv1′2-
mAv1′2- mv12=101.4J;拉力做功为101.4J.
mv12=101.4J;拉力做功为101.4J.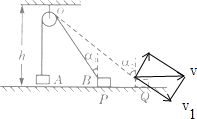
本题中由于拉力是变力,故无法直接用功的公式计算,可以使用动能定理求出拉力的功;
首先由速度的合成与分解求得A上升的速度,由几何关系可求得物体A上升的高度,则由动能定理可求得拉力的功.
考点:动能定理的应用;运动的合成和分解;功的计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
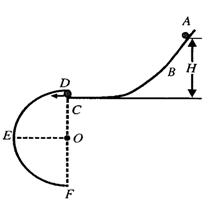
 倍。开始时两球间距、球2与洞口间距均为L。求:
倍。开始时两球间距、球2与洞口间距均为L。求:
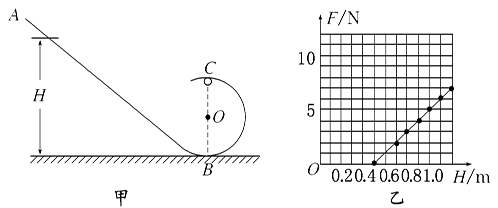

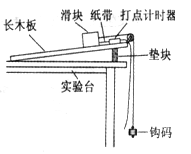

 和
和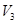 ,1、3两点之间距离为s,重力加速度为g,探究结果的表达式是。(用相应的符号表示)
,1、3两点之间距离为s,重力加速度为g,探究结果的表达式是。(用相应的符号表示)