题目内容
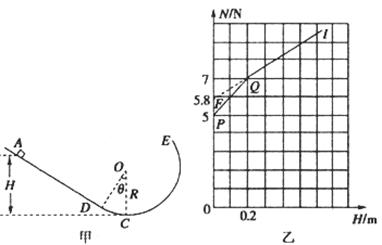
在半径R=5 000 km的某星球表面,宇航员做了如下实验,实验装置如图甲所示.竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成,将质量m=0.2 kg的小球,从轨道AB上高H处的某点由静止滑下,用力传感器测出小球经过C点时对轨道的压力F,改变H的大小,可测出相应的F大小,F随H的变化关系如图乙所示.求: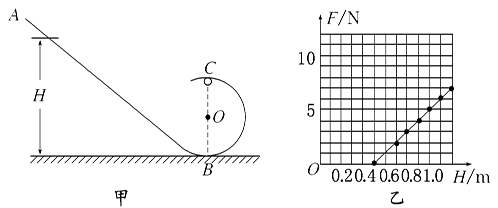
(1)圆轨道的半径及星球表面的重力加速度.
(2)该星球的第一宇宙速度.
(1)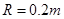 ,
,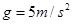 (2)5000m/s
(2)5000m/s
解析试题分析:(1)小球从高度A滑到轨道最高点C点,根据动能定理有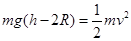 ,通过最高点C点时,重力和轨道向下的弹力提供向心力有
,通过最高点C点时,重力和轨道向下的弹力提供向心力有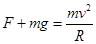 整理可得
整理可得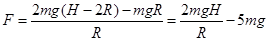
观察乙图可知,当F=0时,H=0.5m,即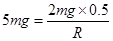 ,带入计算得
,带入计算得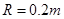
斜率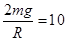 解得,
解得,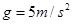
(2)该星球第一宇宙速度即该星球表面近地卫星的线速度,根据万有引力提供向心力有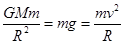
带入得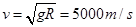
考点:动能定理 圆周运动 万有引力与航天

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图3所示,静止的小球沿不同的轨道由同一位置滑到水平桌面上,轨道高度为h,桌面距地面高为H,物体质量为m,则以下说法正确的是( )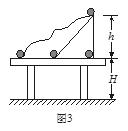
| A.小球沿竖直轨道下滑到桌面上的过程,重力做功最少 |
| B.小球沿曲线轨道下滑到桌面上的过程,重力做功最多 |
| C.以桌面为参考面,小球的重力势能的减少量为mgh |
| D.以地面为参考面,小球的重力势能的减少量为mg(H+h) |
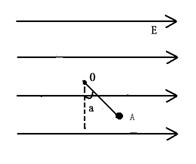
 =0.20,重力加速度g=10m/s2 ,求:
=0.20,重力加速度g=10m/s2 ,求: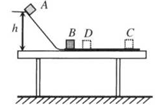
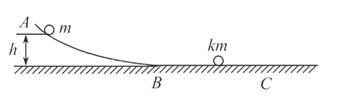
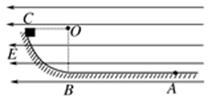
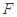 使B以
使B以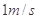 匀速的由P运动到Q,P、Q处绳与竖直方向的夹角分别为α1=37°,α2=53°.滑轮离光滑水平面高度
匀速的由P运动到Q,P、Q处绳与竖直方向的夹角分别为α1=37°,α2=53°.滑轮离光滑水平面高度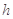 =2.4m,已知
=2.4m,已知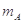 =10
=10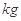 ,
,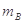 =20
=20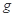 取
取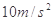 )
)
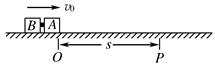
 一起从O点滑出,滑行一段距离后到达P点,速度变为
一起从O点滑出,滑行一段距离后到达P点,速度变为 ,此时炸药爆炸使木块A、B脱离,发现木块B立即停在原位置,木块A继续沿水平方向前进.已知O、P两点间的距离为s,炸药爆炸时释放的化学能均全部转化为木块的动能,爆炸时间很短可以忽略不计.求:
,此时炸药爆炸使木块A、B脱离,发现木块B立即停在原位置,木块A继续沿水平方向前进.已知O、P两点间的距离为s,炸药爆炸时释放的化学能均全部转化为木块的动能,爆炸时间很短可以忽略不计.求: