题目内容
(1 0分)一种弹珠游戏如图,球1以初速v0出发,与球2发生弹性正碰,使球2进入洞中,但球1不能进洞。已知两球的质量比m1: m2=3:2,两球所受阻力均为自身重力的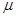 倍。开始时两球间距、球2与洞口间距均为L。求:
倍。开始时两球间距、球2与洞口间距均为L。求:
①两球碰撞完成的瞬间二者速度大小之比;
②为了能够完成任务,球1的初速度v0的最小值。
①v1:v2=1:6 ②v0= 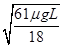
解析试题分析:①两球碰撞过程满足动量守恒定律和机械能守恒定律,设碰前瞬间球1的速度为v
m1v=m1v1+m2v2
m1v2/2=m1v12/2+m2v22/2
可得:v1=v/5,v2=6v/5
两者速度之比v1:v2=1:6
②当球1初速度最小时,碰后小球2应刚好落入洞中有
µm2gL=m2v22/2
碰前球1做减速运动
-µm1gL=m1v2/2- m1v02/2
可得 v0= 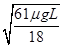
考点:本题考查动量守恒定律和动能定理的应用。

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
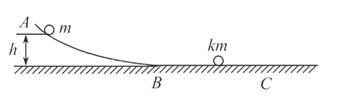
质量为m的小球,从离桌面H高处由静止下落,桌面离地面高度为h,如图所示,若以桌面为参考平面,那么小球落地时的重力势能及整个下落过程中重力势能的变化分别是 ( )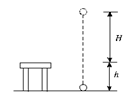
| A. mgh,减少mg(H-h) |
| B. mgh,增加mg(H+h) |
| C.-mgh,增加mg(H-h) |
| D.-mgh,减少mg(H+h) |

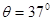 ,劲度系数
,劲度系数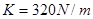 的轻质光滑弹簧平行于传送带放置,下端固定在水平地面上,另一端自由状态时位于Q点。小滑块质量
的轻质光滑弹簧平行于传送带放置,下端固定在水平地面上,另一端自由状态时位于Q点。小滑块质量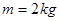 ,放置于传送带P点,滑块与传送带间的滑动摩擦因数
,放置于传送带P点,滑块与传送带间的滑动摩擦因数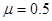 。 已知传送带足够长,最大静摩擦力可认为和滑动摩擦力相等, 整个过程中小滑块未脱离传送带,弹簧处于弹性限度内,弹簧的弹性势能
。 已知传送带足够长,最大静摩擦力可认为和滑动摩擦力相等, 整个过程中小滑块未脱离传送带,弹簧处于弹性限度内,弹簧的弹性势能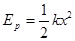 ,x为弹簧的形变量 (重力加速度g=10m/s2,sin370=0.6,cos370=0.8)
,x为弹簧的形变量 (重力加速度g=10m/s2,sin370=0.6,cos370=0.8)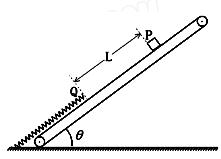
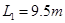 ,求小物块滑行的最大距离
,求小物块滑行的最大距离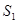 ;
;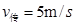 速度逆时针传动,将小滑块无初速放在P点, PQ距离
速度逆时针传动,将小滑块无初速放在P点, PQ距离 ,求小物块滑行的最大距离
,求小物块滑行的最大距离 。
。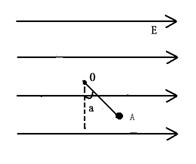
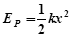 。求:
。求: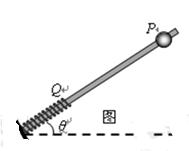
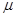 =0.20,重力加速度g=10m/s2 ,求:
=0.20,重力加速度g=10m/s2 ,求:
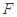 使B以
使B以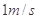 匀速的由P运动到Q,P、Q处绳与竖直方向的夹角分别为α1=37°,α2=53°.滑轮离光滑水平面高度
匀速的由P运动到Q,P、Q处绳与竖直方向的夹角分别为α1=37°,α2=53°.滑轮离光滑水平面高度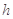 =2.4m,已知
=2.4m,已知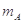 =10
=10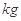 ,
,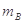 =20
=20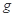 取
取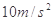 )
)