Question

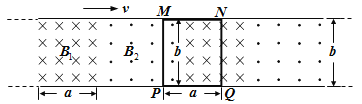
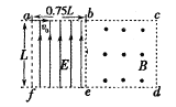
【题目】如图所示，将一矩形区域abcdef分为两个矩形区域，abef区域充满匀强电场，场强为E，方向竖直向上；bcde区域充满匀强磁场，磁感应强度为B，方向垂直纸面向外。be为其分界线。af、bc长度均为L，ab长度为0.75L。现有一质量为m、电荷量为e的电子（重力不计）从a点沿ab方向以初速度v0射入电场。已知电场强度，sin37°＝0.6，cos37°＝0.8.求：

(1)该电子从距离b点多远的位置进入磁场；

(2)若要求电子从cd边射出，所加匀强磁场磁感应强度的最大值；

(3)若磁感应强度的大小可以调节，则cd边上有电子射出部分的长度为多少。

Answer 1

【答案】(1)；(2)；(3)。

【解析】

(1)电子在电场中做类似平抛运动，有

0.75L＝v0t

eE＝ma

得

即该电子从距b点处进入磁场 .

（2）粒子进入磁场时，速度方向与be边夹角的正切值

tanθ＝

θ＝37°

电子进入磁场时的速度为

设电子运动轨迹刚好与cd边相切时，半径最小为r1，则由几何关系知

r1＋r1cos37°＝L

解得

由可得对应的最大磁感应强度

B＝

(3)设电子运动轨迹刚好与de边相切时，半径为r2，则

r2＝r2sin37°＋L，

解得

r2＝L

又r2cosθ＝L，故切点刚好为d点

电子从cd边射出的长度为

△y＝L＋r1sin37°＝