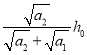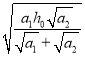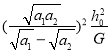题目内容
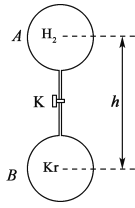
【题目】某同学在研究性学习中用如图装置来验证机械能守恒定律，轻绳两端系着质量相等的物体A、B，物体B上放一金属片C，铁架台上固定一金属圆环，圆环处在物体B的正下方，系统静止时，金属片C与圆环间的高度差为h，由静止释放后，系统开始运动，当物体B穿过圆环时，金属片C被搁置在圆环上，两光电门固定在铁架台P1、P2处，通过数字计时器可测出物体B通过P1、P2这段距离的时间。
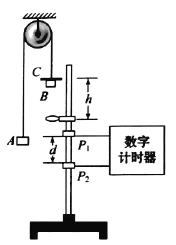
（1）若测得P1、P2之间的距离为d，物体B通过这段距离的时间为t，则物体B刚穿过圆环后的速度v=______。
（2）若物体A、B的质量均用M表示，金属片C的质量用m表示，该实验中验证下面__________（填正确选项的序号）等式成立，即可验证牛顿第二定律。
A. 
B. 
C. 
D. 
（3）本实验中的测量仪器除了刻度尺、数字计时器外，还需要___________。
（4）若M>>m，改变金属片C的质量m，使物体B由同一高度落下穿过圆环，记录各次的金属片C的质量m，以及物体B通过P1、P2这段距离的时间t，以mg为横轴，以__________（选填“
”或“
”）为纵轴，通过描点作出的图线是一条过原点的直线。
【答案】
C 天平 
【解析】
（1）[1]B通过圆环后将匀速通过光电门，则B刚穿过圆环后的速度为：
。
（2）[2]选C。设绳子拉力大小为F，对A由牛顿第二定律得：
对B与C整体下落h的过程，由牛顿第二定律得：
再由运动学公式应有：
，联立以上各式可得：
所以C正确。
（3）[3]根据上面的表达式可知需要已知金属片C的质量，所以还需要的器材是天平。
（4）[4]在释放至金属片C被搁置在圆环上的过程中，分别对A和B、C由牛顿第二定律可得：对A有
对B和C有
再由匀变速直线运动公式应有
，
联立解得：
因为M>>m，则
所以，以mg为横轴，以为纵轴的图线是一条过原点的直线。
