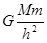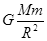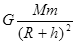题目内容
一卫星绕某一行星表面附近做匀速圆周运动，其线速度大小为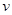
，假设宇航员在该行星表面上用弹簧测力计测量一质量为m的物体的重力，物体静止时，弹簧测力计的示数为F，已知引力常量为G，则这颗行星的质量为( )
A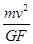． | B． | C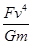． | D． |
D
解析试题分析：卫星绕着该行星以第一宇宙速度的大小运行，该行星点的第一宇宙速度可表示为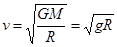
；根据力平衡的知识有F=mg，联系以上两式可得这颗行星的质量为，因此选项D正确。
考点：本题考查第一宇宙速度，天体质量的测量。
如图，带正电的点电荷固定于Q点，电子在库仑力作用下，做以Q为焦点的椭圆运动．M、P、N为椭圆上的三点，P点是轨道上离Q最近的点．电子在从M经P到达N点的过程中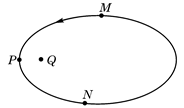
| A．速率先增大后减小 |
| B．速率先减小后增大 |
| C．电势能先减小后增大 |
| D．电势能先增大后减小 |
“嫦娥三号”探月卫星计划于2013年下半年在西昌卫星发射中心发射，将实现“落月”的新阶段。已知月球绕地球做圆周运动的半径为r1、周期为T1；“嫦娥三号”探月卫星绕月球做圆周运动的半径为r2、周期为T2。引力常量为G，不计周围其他天体的影响，下列说法正确的是
| A．根据题目条件能求出“嫦娥三号”探月卫星的质量 |
| B．根据题目条件能求出地球的密度 |
| C．根据题目条件能求出地球与月球之间的引力 |
D．根据题目条件可得出 |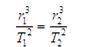
太空中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式：一种是三颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行；另一种形式是三颗星位于等边三角形的三个顶点上，并沿外接于等边三角形的圆形轨道运行。设这三个星体的质量均为M，并设两种系统的运动周期相同，则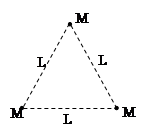
A．直线三星系统运动的线速度大小为 |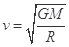
B．此三星系统的运动周期为 |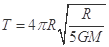
C．三角形三星系统中星体间的距离为 |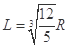
D．三角形三星系统的线速度大小为 |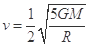
举世瞩目的“神舟”十号航天飞船的成功发射，显示了我国航天事业取得的巨大成就．已知地球的质量为M，引力常量为G，设飞船绕地球做匀速圆周运动的轨道半径为r，则飞船在圆轨道上运行的速率为
A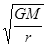． | B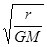． | C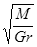． | D． |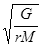
已知地球质量大约是月球质量的81倍，地球半径大约是月球半径的4倍，不考虑地球、月球自转的影响，由以上数据可推算出
| A．地球的平均密度与月球的平均密度之比约为9∶8 |
| B．地球表面重力加速度与月球表面重力加速度之比约为9∶4 |
| C．靠近地球表面沿圆轨道运行的航天器的周期与靠近月球表面沿圆轨道运行的航天器的周期之比约为8∶9 |
| D．靠近地球表面沿圆轨道运行的航天器线速度与靠近月球表面沿圆轨道运行的航天器线速度之比约为81∶4 |
如图所示，如果把水星和金星绕太阳的运动视为匀速圆周运动，从水星与金星在一条直线上开始计时，若天文学家测得在相同时间内水星转过的角度为θ1，金星转过的角度为θ2(θ1、θ2均为锐角)，则由此条件可求得（ ）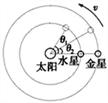
| A．水星和金星绕太阳运动的周期之比 |
| B．水星和金星的密度之比 |
| C．水星和金星到太阳中心的距离之比 |
| D．水星和金星绕太阳运动的向心加速度大小之比 |
设想我国宇航员随“嫦娥”号登月飞船贴近月球表面做匀速圆周运动，宇航员测出飞船绕行n圈所用的时间为t. 登月后，宇航员利用身边的弹簧秤测出质量为m的物体重力为G1. 已知引力常量为G，根据以上信息可得到（ ）
| A．月球的自转周期 | B．飞船的质量 |
| C．月球的第一宇宙速度 | D．月球的密度 |