题目内容
15. 如图1,在两块相同的竖直木板A、B之间有重为G=30N的物体,用两个大小相同的力F1、F2垂直压木板,物体与木板间的动摩擦因数μ=0.5,不计木板的重力,滑动摩擦力的大小等于最大静摩擦力.
如图1,在两块相同的竖直木板A、B之间有重为G=30N的物体,用两个大小相同的力F1、F2垂直压木板,物体与木板间的动摩擦因数μ=0.5,不计木板的重力,滑动摩擦力的大小等于最大静摩擦力.(1)已知F1=F2=40N,若把物体沿板竖直向上拉出,求所需拉力的最小值.
(2)已知F1=F2=40N,若把物体沿板水平拉出(垂直纸面方向),求所需拉力的最小值.
(3)如图2,现调整F1、F2大小使两木板在竖直平面内转到与水平方向成37°角时,物体处于平衡,此时F1=18N.若用平行于木板的力把物体沿板向上拉出,求拉力F的最小值.
分析 (1)对物体受力分析,由受力平衡条件,即可求解;
(2)根据滑动摩擦力的公式,结合受力平衡,即可求解.
(3)先求出滑动摩擦力,再由平衡条件解答.
解答 解:(1)竖直向上拉出,则拉力 F=G+f1+f2=70N
(2)将物体水平拉出,沿板面受力分析如下图所示.
得拉力最小值为 F=$\sqrt{{G^2}+{{(2f)}^2}}$=50N
(3)把物体沿板向上拉出,物体与木板A之间的滑动摩擦力
f1=μF1=0.5×18N=9N
物体与木板B之间的滑动摩擦力
f2=μ(F1+Gcos37°)=0.5×(18+24)N=21N
则拉力 F=Gsin37°+f1+f2=48N
答:(1)所需拉力的最小值是70N.
(2)所需拉力的最小值是50N.
(3)拉力F的最小值是48N.
点评 此题要掌握滑动摩擦力大小计算公式,掌握平衡方程的应用,注意正确的受力分析,及三角函数的正确运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 一带电微粒M在相互垂直的匀强电场、匀强磁场中作匀速圆周运动,匀强电场竖直向上,匀强磁场水平且垂直纸面向里,如图所示,下列说法正确的是( )
一带电微粒M在相互垂直的匀强电场、匀强磁场中作匀速圆周运动,匀强电场竖直向上,匀强磁场水平且垂直纸面向里,如图所示,下列说法正确的是( )
 一带电微粒M在相互垂直的匀强电场、匀强磁场中作匀速圆周运动,匀强电场竖直向上,匀强磁场水平且垂直纸面向里,如图所示,下列说法正确的是( )
一带电微粒M在相互垂直的匀强电场、匀强磁场中作匀速圆周运动,匀强电场竖直向上,匀强磁场水平且垂直纸面向里,如图所示,下列说法正确的是( )| A. | 沿垂直纸面方向向里看,微粒M的绕行方向为逆时针方向 | |
| B. | 沿垂直纸面方向向里看,微粒M的绕行方向为顺时针方向 | |
| C. | 在微粒旋转一周的时间内电场力做功为零 | |
| D. | 运动过程中外力对微粒作功的代数和为零,故机械能守恒 |
10. A、B两物体在同一直线上从某点开始计时的速度图象如图中的A、B所示,则由图可知,在0-t2时间内( )
A、B两物体在同一直线上从某点开始计时的速度图象如图中的A、B所示,则由图可知,在0-t2时间内( )
 A、B两物体在同一直线上从某点开始计时的速度图象如图中的A、B所示,则由图可知,在0-t2时间内( )
A、B两物体在同一直线上从某点开始计时的速度图象如图中的A、B所示,则由图可知,在0-t2时间内( )| A. | 在t1时刻B运动方向改变 | |
| B. | 在t2时刻,A、B的速度相同,加速度也相同 | |
| C. | A、B运动始终同向,B比A运动的快 | |
| D. | A、B的加速度始终同向,B比A的加速度大 |
20.某同学在“探究小车速度随时间变化规律“实验中,由打点计时器得到表示小车运动过程的一条清晰纸带如图1所示,
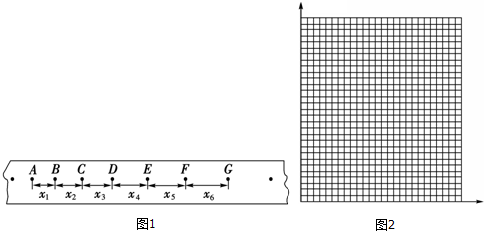
(1)已知电火花式打点计时器所用交流电的周期为T,纸带上各计数点的间距如图2,其中每相邻两点之间还有4个记录点未画出,计算小车运动加速度的表达式为a=$\frac{({x}_{4}+{x}_{5}+{x}_{6})-({x}_{1}+{x}_{2}+{x}_{3})}{9{T}^{2}}$
(2)某同学量得x1=7.05cm、x2=7.68cm、x3=8.33cm、x4=8.95cm、x5=9.61cm、x6=10.23cm.已知T=0.02s,由此计算出打点计时器打下B、C、D、F时小车的瞬时速度,则打点计时器打下E点时小车的瞬时速度vE=0.928m/s(小数点后保留三位数字).
(3)以A点为计时起点,在坐标图中合理地选择标度,画出小车的v-t图象,并利用该图象求出物体的加速度a=0.64m/s2(结果保留两位有效数字).

(1)已知电火花式打点计时器所用交流电的周期为T,纸带上各计数点的间距如图2,其中每相邻两点之间还有4个记录点未画出,计算小车运动加速度的表达式为a=$\frac{({x}_{4}+{x}_{5}+{x}_{6})-({x}_{1}+{x}_{2}+{x}_{3})}{9{T}^{2}}$
(2)某同学量得x1=7.05cm、x2=7.68cm、x3=8.33cm、x4=8.95cm、x5=9.61cm、x6=10.23cm.已知T=0.02s,由此计算出打点计时器打下B、C、D、F时小车的瞬时速度,则打点计时器打下E点时小车的瞬时速度vE=0.928m/s(小数点后保留三位数字).
| 位置 | B | C | D | E | F |
| 速度(m•s-1) | 0.737 | 0.801 | 0.864 | 0.992 |
4.下列说法正确的是( )
| A. | 电子的衍射现象说明实物粒子具有波动性 | |
| B. | 光的波长越小,光子的能量越小 | |
| C. | 在放射性元素中掺杂某种稳定元素并大幅度地降低它的温度就可以减小它的半衰期 | |
| D. | 在α、β、γ这三种射线中,γ射线的穿透能力最强,α射线的电离能力最强 |
 如图所示电路中,R1=6Ω,R2=12Ω,R3=3Ω,C=30μF,当开关S断开,电路稳定时,电源总功率为4W,当开关S闭合,电路稳定时,电源总功率为8W,求:
如图所示电路中,R1=6Ω,R2=12Ω,R3=3Ω,C=30μF,当开关S断开,电路稳定时,电源总功率为4W,当开关S闭合,电路稳定时,电源总功率为8W,求: