题目内容
20.某同学在“探究小车速度随时间变化规律“实验中,由打点计时器得到表示小车运动过程的一条清晰纸带如图1所示,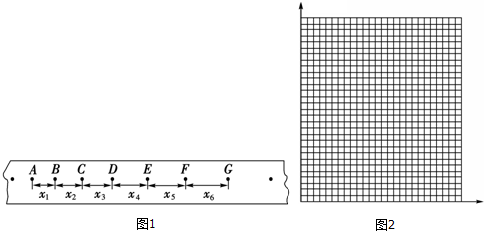
(1)已知电火花式打点计时器所用交流电的周期为T,纸带上各计数点的间距如图2,其中每相邻两点之间还有4个记录点未画出,计算小车运动加速度的表达式为a=$\frac{({x}_{4}+{x}_{5}+{x}_{6})-({x}_{1}+{x}_{2}+{x}_{3})}{9{T}^{2}}$
(2)某同学量得x1=7.05cm、x2=7.68cm、x3=8.33cm、x4=8.95cm、x5=9.61cm、x6=10.23cm.已知T=0.02s,由此计算出打点计时器打下B、C、D、F时小车的瞬时速度,则打点计时器打下E点时小车的瞬时速度vE=0.928m/s(小数点后保留三位数字).
| 位置 | B | C | D | E | F |
| 速度(m•s-1) | 0.737 | 0.801 | 0.864 | 0.992 |
分析 (1)根据逐差法规律可明确加速度的计算式.
(2)在匀变速直线运动中,时间中点的速度等于该过程中的平均速度,可以求出E速度大小.
(3)利用描点法可画出速度-时间图象.
(4)根据v-t图象的物理意义可知,图象的斜率表示加速度大小.
解答 解:(1)由逐差法可知,加速度的计算式a=$\frac{({x}_{4}+{x}_{5}+{x}_{6})-({x}_{1}+{x}_{2}+{x}_{3})}{9{T}^{2}}$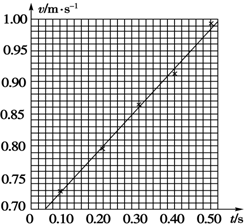
(2)根据匀变速直线运动某时刻的瞬时速度等于一段时间内的平均速度,所以有:
vD=$\frac{{x}_{CE}}{2T}=\frac{{x}_{3}+{x}_{4}}{2T}$═$\frac{(8.33+8.95)×{10}^{-2}m}{2×0.1s}$=0.864m/s
vE=$\frac{{x}_{DF}}{2T}=\frac{{x}_{4}+{x}_{5}}{2T}$=$\frac{(8.95+9.61)×{10}^{-2}m}{2×0.1s}$=0.928m/s
(3)利用描点法可画出速度-时间图象:
(4)在v-t图象中,图象的斜率表示加速度的大小,所以有:
a=$\frac{△v}{△t}$=0.64 m/s2.
故答案为:(1)$\frac{({x}_{4}+{x}_{5}+{x}_{6})-({x}_{1}+{x}_{2}+{x}_{3})}{9{T}^{2}}$;(2)0.928;(3)如上图;(4)0.64
点评 对于实验器材的选取一是根据实验目的进行,二是要进行动手实验,体会每种器材的作用;考查了有关纸带处理的基本知识,平时要加强基础实验的实际操作,提高操作技能和数据处理能力.要注意单位的换算和有效数字的保留;同时注意利用图象来解决问题.

 阅读快车系列答案
阅读快车系列答案| A. | 只要两个物体接触就一定有弹力产生 | |
| B. | 有摩檫力就一定有弹力产生 | |
| C. | 挂在电线下面的电灯受到向上的拉力,是因为电线发生微小的形变而产生的 | |
| D. | 形变大的物体产生的弹力一定比形变小的物体产生的弹力大 |
 作用在同一物体上的三个力F1、F2、F3,现将三个共点力矢量首尾相连后,得到如图所示三角形,则这三个力的合力为( )
作用在同一物体上的三个力F1、F2、F3,现将三个共点力矢量首尾相连后,得到如图所示三角形,则这三个力的合力为( )| A. | 0 | B. | 2F1 | C. | 2F2 | D. | 2F3 |

| A. | 电势φA>φB,场强EA<EB | |
| B. | 电势φA>φB,场强EA>EB | |
| C. | 将电荷+q分别放在A、B两点时具有的电势能EpA>EpB | |
| D. | 将电荷-q从A点移到B点静电力做了负功 |
 如图所示,质量均可忽略的轻绳与轻杆,A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计),B端吊一重物.现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前( )
如图所示,质量均可忽略的轻绳与轻杆,A端用铰链固定,滑轮在A点正上方(滑轮大小及摩擦均可不计),B端吊一重物.现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前( )| A. | 绳子拉力不变 | B. | 绳子拉力减小 | C. | AB杆受力增大 | D. | AB杆受力减小 |
| A. | 在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫微元法 | |
| B. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法 | |
| C. | 在探究加速度、力和质量三者之间的关系时,先保持质量不变研究加速度与 力的关系,再保持力不变研究加速度与质量的关系,该实验应用了类比法 | |
| D. | 笛卡尔将实验和逻辑推理和谐的结合起来,从而发展了人类的科学思维方式和科学的研究方法----理想实验法 |
 如图所示,质量为m的小滑块从O点以速度v0沿水平面向左运动,小滑块撞击弹簧后被弹簧弹回并最终静止于O点,则运动过程中弹簧获得的最大弹性势能是.
如图所示,质量为m的小滑块从O点以速度v0沿水平面向左运动,小滑块撞击弹簧后被弹簧弹回并最终静止于O点,则运动过程中弹簧获得的最大弹性势能是.| A. | $\frac{1}{3}$mv02 | B. | $\frac{1}{4}$mv02 | C. | $\frac{1}{6}$mv02 | D. | $\frac{1}{8}$mv02 |
 如图1,在两块相同的竖直木板A、B之间有重为G=30N的物体,用两个大小相同的力F1、F2垂直压木板,物体与木板间的动摩擦因数μ=0.5,不计木板的重力,滑动摩擦力的大小等于最大静摩擦力.
如图1,在两块相同的竖直木板A、B之间有重为G=30N的物体,用两个大小相同的力F1、F2垂直压木板,物体与木板间的动摩擦因数μ=0.5,不计木板的重力,滑动摩擦力的大小等于最大静摩擦力. 两束平行的细激光束,垂直于半圆柱玻璃的平面射到半圆柱玻璃上,如图所示.已知其中一条光线沿直线穿过玻璃,它的入射点是O;另一条光线的入射点为A,穿过玻璃后两条光线交于P点.已知玻璃截面的圆半径为R,OA=$\frac{R}{2}$,OP=$\sqrt{3}$R.求:
两束平行的细激光束,垂直于半圆柱玻璃的平面射到半圆柱玻璃上,如图所示.已知其中一条光线沿直线穿过玻璃,它的入射点是O;另一条光线的入射点为A,穿过玻璃后两条光线交于P点.已知玻璃截面的圆半径为R,OA=$\frac{R}{2}$,OP=$\sqrt{3}$R.求: