题目内容
有两颗行星A、B，在两个行星表面附近各有一颗卫星，如果这两颗卫星运动的周期相等，下列说法正确的是（ ）
| A．行星A、B表面重力加速度之比等于它们的半径之比 |
| B．两卫星的线速度一定相等 |
| C．行星A、B的质量和半径一定相等 |
| D．行星A、B的密度一定相等 |
A、根据万有引力提供向心力G
=m
R，得：GM=
在行星表面的物体受到重力等于万有引力mg=G
，得：g=
=
，
所以行星A、B表面重力加速度之比等于它们的半径之比，故A正确．
B、根据线速度与周期和半径的关系得v=
，由于行星的半径未知，故两卫星的线速度不能确定是否相等，故B错误．
C、由G
=m
R，得：M=
，由于行星的半径未知，故行星的质量不能确定，故C错误．
D、行星的体积为V=
πR3，所以密度为：ρ=
=
=
，故行星A、B的密度一定相等，故D正确．
故选：AD．
| Mm |
| R2 |
| 4π2 |
| T2 |
| 4π2R3 |
| T2 |
在行星表面的物体受到重力等于万有引力mg=G
| Mm |
| R2 |
| GM |
| R2 |
| 4π2R |
| T2 |
所以行星A、B表面重力加速度之比等于它们的半径之比，故A正确．
B、根据线速度与周期和半径的关系得v=
| 2πR |
| T |
C、由G
| Mm |
| R2 |
| 4π2 |
| T2 |
| 4π2R3 |
| GT2 |
D、行星的体积为V=
| 4 |
| 3 |
| M |
| V |
| ||
|
| 3π |
| GT2 |
故选：AD．
练习册系列答案
导学全程练创优训练系列答案
相关题目
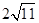倍）利用太阳能发电，然后通过微波持续不断地将电力输送到地面，这样就建成了太阳能发电站。求卫星在地球同步轨道上向心加速度的大小（答案保留两位有效数字）；
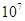m，它与另一颗同质量的同步轨道卫星（轨道半径为4．2×