题目内容
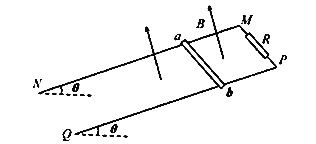
【题目】如图所示，在真空室内的P点，能沿平行纸面向各个方向不断发射电荷量为＋q、质量为m的粒子(不计重力)，粒子的速率都相同．ab为P点附近的一条水平直线，P到直线ab的距离PC＝L，Q为直线ab上一点，它与P点相距PQ＝
.当直线ab以上区域只存在垂直纸面向里、磁感应强度为B的匀强磁场时，水平向左射出的粒子恰到达Q点；当ab以上区域只存在平行该平面的匀强电场时，所有粒子都能到达ab直线，且它们到达ab直线时动能都相等，其中水平向左射出的粒子也恰好到达Q点．已知sin 37°＝0.6，cos 37°＝0.8，求：
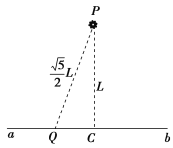
(1)粒子的发射速率；
(2)PQ两点间的电势差；
(3)仅有磁场时，能到达直线ab的粒子所用最长时间和最短时间。
【答案】(1) 
(2) 
(3) 
【解析】
（1）当只存在匀强磁场时，α粒子由洛伦兹力提供向心力而做匀速圆周运动，画出α粒子的运动轨迹，由几何知识求出α粒子做匀速圆周运动的半径，由牛顿第二定律求出α粒子的发射速率；
（2）当只存在匀强电场时，α粒子做类平抛运动，由牛顿第二定律和运动学结合求解PQ两点间的电势差；
（3）当仅加上述磁场时，根据几何知识确定出轨迹的圆心角，然后求出能到达直线ab的粒子所用最长时间和最短时间．
（1）设粒子做匀速圆周运动的半径为R，过O作PQ的垂线交PQ于A点，如图所示：
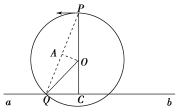
由几何知识可得
代入数据可得粒子轨迹半径
洛伦兹力提供向心力Bqv＝m
解得粒子发射速度为v＝
（2）真空室只加匀强电场时，由粒子到达ab直线的动能相等，可知ab为等势面，电场方向垂直ab向下．水平向左射出的粒子经时间t到达Q点，在这段时间内
＝L＝
at2
式中a＝
U＝Ed
解得电场强度的大小为U＝
（3）只有磁场时，粒子以O1为圆心沿圆弧PD运动，当圆弧和直线ab相切于D点时，粒子速度的偏转角最大，对应的运动时间最长，如图所示．据图有
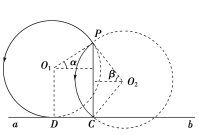
sin α＝
解得α＝37°
故最大偏转角γmax＝233°
粒子在磁场中运动最大时长
式中T为粒子在磁场中运动的周期．
粒子以O2为圆心沿圆弧PC运动的速度偏转角最小，对应的运动时间最短．据图有
sin β＝
解得β＝53°
速度偏转角最小为γmin＝106°
故最短时长
