题目内容
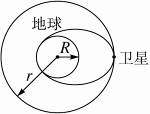
两颗地球卫星A、B均绕地球做圆周运动，且它们的轨道在同一平面内，卫星B离地球较近，若在运行过程中A、B间的最远距离与最近距离之比为5：3，则（ ）
| A．A、B的线速度之比为1：4 | B．A、B的线速度之比为1：2 |
| C．A、B的周期之比为1：4 | D．A、B的周期之比为8：1 |
两颗地球卫星A、B均绕地球做圆周运动，设卫星A、B的轨道半径是rA，rB．
卫星B离地球较近，若在运行过程中A、B间的最远距离与最近距离之比为5：3，
（rA+rB）：（rA-rB）=5：3
解得：rA=4rB ．
卫星绕地球做匀速圆周运动，靠万有引力提供向心力，
=
=m
A、线速度v=
，所以A、B的线速度之比为1：2．故A错误，B正确；
C、周期T=2π
，所以A、B的周期之比为8：1，故C错误，D正确；
故选：BD．
卫星B离地球较近，若在运行过程中A、B间的最远距离与最近距离之比为5：3，
（rA+rB）：（rA-rB）=5：3
解得：rA=4rB ．
卫星绕地球做匀速圆周运动，靠万有引力提供向心力，
| GMm |
| r2 |
| mv2 |
| r |
| 4π2r |
| T2 |
A、线速度v=
|
C、周期T=2π
|
故选：BD．
练习册系列答案
阅读快车系列答案
相关题目
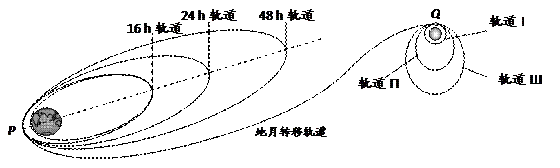
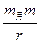．为使“嫦娥一号”卫星在近月点Q进行第一次制动后能成为月球的卫星，且与月球表面的距离不小于圆形工作轨道I的高度，最终进入圆形工作轨道，其第一次制动后的速度大小应满足什么条件？
