题目内容
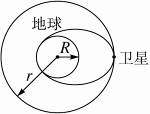
开普勒从1609年~1619年发表了著名的开普勒行星运动三定律.第一定律:所有的行星分别在大小不同的椭圆轨道上围绕太阳运动,太阳在这个椭圆的一个焦点上;第二定律:太阳和行星的连线在相等的时间内扫过的面积相等;第三定律:所有行星的椭圆轨道的半长轴的三次方跟公转周期的平方的比值相等.实践证明,开普勒三定律也适用于人造地球卫星的运动.如果人造地球卫星沿半径为r的圆轨道绕地球运动,当开启制动发动机后,卫星转移到与地球相切的椭圆形轨道,如图所示.问在这之后,卫星多长时间着陆?空气阻力不计,地球半径为R,地球表面重力加速度为g.

??t=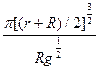
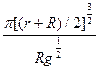
??设卫星在地球表面运行时周期为T卫星由圆轨道转移到椭圆轨道,其半长轴为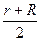 ,设周期为T′,据开普勒第三定律有
,设周期为T′,据开普勒第三定律有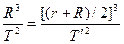 卫星落地时间t=
卫星落地时间t=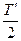 设卫星在地球表面做圆周运动,则mg=mRω2=
设卫星在地球表面做圆周运动,则mg=mRω2=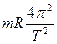 ,T2=
,T2=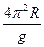 所以T′2=
所以T′2=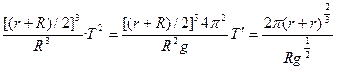 所以t=
所以t=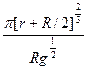 .
.
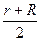 ,设周期为T′,据开普勒第三定律有
,设周期为T′,据开普勒第三定律有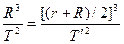 卫星落地时间t=
卫星落地时间t=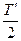 设卫星在地球表面做圆周运动,则mg=mRω2=
设卫星在地球表面做圆周运动,则mg=mRω2=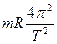 ,T2=
,T2=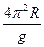 所以T′2=
所以T′2=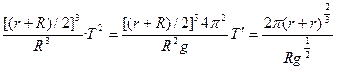 所以t=
所以t=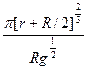 .
.
练习册系列答案
相关题目

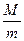 为多大?
为多大?