Question

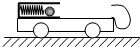
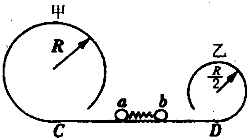
如图所示，在光滑水平面上静置有质量均为m的木板AB和光滑

1

4

圆弧滑块CD，其始端D点切线水平且在木板AB上表面内，它们紧靠在一起，一可视为质点的物块P，质量也为m，从木板AB的右端以初速度v₀滑上木板AB，过B点时速度为

v0

2

，此后又滑上滑块CD，最终恰好能滑到滑块CD圆弧的最高点C处，已知木板AB上表面粗糙，与物块间的动摩擦因数为μ，求：
（1）物块滑到B处时木板的速度v_AB；
（2）木板的长度L；
（3）滑块CD圆弧的半径R．

Answer 1

（1）由点A到点B时，取向左为正．
由动量守恒得mv₀=mv_B+2m?v_AB ，
由题意知：v_B=

v0

2

，解得：v_AB=

v0

4

；
（2）由点A到点B时，由能量守恒定律得：

1

2

mv₀²-

1

2

?2m（

v0

4

）²-

1

2

m（

v0

2

）²=μmgL，
解得：L=

5 v 20

16μg

；
（3）由点D到点C，滑块CD与物块P的水平方向动量守恒，
以滑块的初速度方向为正方向，由动量守恒定律得：m

v0

2

+m

v0

4

=2mv，
由机械能守恒定律得：mgR=

1

2

m（

v0

4

）²+

1

2

m（

v0

2

）²-

1

2

?2mv²，
解得：R=

v 20

64g

；
答：（1）物块滑到B处时木板的速度v_AB=

v0

4

；
（2）木板的长度L=

5 v 20

16μg

；
（3）滑块CD圆弧的半径R=

v 20

64g

．