题目内容
如图所示，甲、乙两光滑圆轨道放置在同一竖直平面内，甲轨道半径是R且为乙轨道半径的2倍，两轨道之间由一光滑水平轨道CD相连，在水平轨道CD上有一轻弹簧被a、b两个小球夹住，但不拴接．如果a、b两个小球的质量均为m，同时释放两小球，且要求a、b都能通过各自的最高点，则弹簧在释放前至少具有多大的弹性势能？
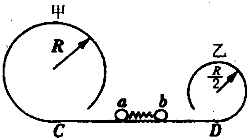
当a球恰能通过最高点时，b球一定通过最高点，此时弹簧在释放前具有的弹性势能最小，设a球到达圆轨道最高点的速度为va，对于a球有：
mag=ma
…①
设a球被弹簧弹开瞬间的速度为v'a，对于a球由机械能守恒定律可得：
mav
=
ma
+mag2R… ②
设b球被弹簧弹开瞬间的速度为v'b，由于a、b两球被弹开时系统动量守恒：mav'a=mbv'b …③
①②③可得：v′a=v′b=
… ④
以a、b两小球以及弹簧组成的系统为研究对象，整个过程中由系统机械能守恒可得：Eq=
mav
+
mbv
… ⑤
由④⑤得弹性势能最小值为：Ep=5mgR
答：弹簧在释放前至少具有5mgR的弹性势能．
mag=ma
| ||
| R |
设a球被弹簧弹开瞬间的速度为v'a，对于a球由机械能守恒定律可得：
| 1 |
| 2 |
| ′ | 2a |
| 1 |
| 2 |
| v | 2a |
设b球被弹簧弹开瞬间的速度为v'b，由于a、b两球被弹开时系统动量守恒：mav'a=mbv'b …③
①②③可得：v′a=v′b=
| 5gR |
以a、b两小球以及弹簧组成的系统为研究对象，整个过程中由系统机械能守恒可得：Eq=
| 1 |
| 2 |
| ′ | 2a |
| 1 |
| 2 |
| ′ | 2b |
由④⑤得弹性势能最小值为：Ep=5mgR
答：弹簧在释放前至少具有5mgR的弹性势能．
练习册系列答案
相关题目
两端同时水平地滑上小车．初速度VA=1.2m/s，VB=0.6m/s，A、B与C间的动摩擦因数都是μ=0.1．A、B、C的质量都相同．最后A、B恰好相遇而未碰撞．g取10m/s2．求：
