题目内容
10.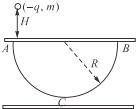 如图所示,平行板电容器的两个极板水平,两板之间固定一个光滑绝缘的半圆形轨道ACB,A、B为半圆轨道的两个端点,且A、B紧靠电容器的上极板,在A端对应位置的极板处开有一个小孔,C是轨道的最低点,半圆轨道半径为R.现使电容器的两板分别带等量异种电荷,使两板之间存在竖直向下的匀强电场,将一个质量为m、电荷量为-q的带电小球,从A点正上方高为H处由静止释放,小球由小孔进入电容器内部并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,下列说法中正确的是( )
如图所示,平行板电容器的两个极板水平,两板之间固定一个光滑绝缘的半圆形轨道ACB,A、B为半圆轨道的两个端点,且A、B紧靠电容器的上极板,在A端对应位置的极板处开有一个小孔,C是轨道的最低点,半圆轨道半径为R.现使电容器的两板分别带等量异种电荷,使两板之间存在竖直向下的匀强电场,将一个质量为m、电荷量为-q的带电小球,从A点正上方高为H处由静止释放,小球由小孔进入电容器内部并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,下列说法中正确的是( )| A. | 当匀强电场的电场强度大小E=$\frac{mg}{q}$时,带电小球在半圆形轨道内做匀速圆周运动 | |
| B. | 当匀强电场的电场强度大小E≤$\frac{mg(H+R)}{qR}$时,带电小球能沿轨道到达最低点 | |
| C. | 当匀强电场的电场强度大小E≤$\frac{mg(H+R)}{3qR}$时,带电小球能沿轨道到达最低点 | |
| D. | 将电容器的下极板向下移动一小段距离,则带电小球到达最低点C时的速率增大 |
分析 当小球的重力与电场力平衡,小球进入轨道,靠弹力提供向心力,做匀速圆周运动.分析在最低点小球的受力情况,根据动能定律,圆周运动的条件,求解最小电场强度;电容器极板间距离的增大,电场强度不变.
解答 解:A、当小球的重力与电场力平衡,小球进入轨道,靠弹力提供向心力,做匀速圆周运动.即mg=Eq,E=$\frac{mg}{q}$,故A正确;
BC、设小球到达最低点的最小速度为v,则有qE-mg=m$\frac{{v}^{2}}{R}$,由动能定理得,mg(R+H)-qER=$\frac{1}{2}\\;\\;\$mv2-0,解得电场强度的最小值E=$\frac{mg(2H+3R)}{3qR}$,故C正确,B错误;
D、将电容器的下极板向下移动一小段距离,Q不变,E不变,小球的受力不变,故达到C点的速率不变;故D错误;
故选:AC
点评 本题考查了带电小球在电场和重力场中的运动,综合运用了动能定理、牛顿第二定律等知识,综合性强,对学生的能力要求较高.

练习册系列答案
相关题目
8. 如图所示,光滑斜面与水平面成α角α=30°,斜面上一根长为l=0.30m的轻杆,一端系住质量为0.2kg的小球,另一端固定在O点,现将轻杆拉直至水平位置,然后给小球一沿着平板并与轻杆垂直的初速度v0=3.0m/s,g=10m/s2,则( )
如图所示,光滑斜面与水平面成α角α=30°,斜面上一根长为l=0.30m的轻杆,一端系住质量为0.2kg的小球,另一端固定在O点,现将轻杆拉直至水平位置,然后给小球一沿着平板并与轻杆垂直的初速度v0=3.0m/s,g=10m/s2,则( )
 如图所示,光滑斜面与水平面成α角α=30°,斜面上一根长为l=0.30m的轻杆,一端系住质量为0.2kg的小球,另一端固定在O点,现将轻杆拉直至水平位置,然后给小球一沿着平板并与轻杆垂直的初速度v0=3.0m/s,g=10m/s2,则( )
如图所示,光滑斜面与水平面成α角α=30°,斜面上一根长为l=0.30m的轻杆,一端系住质量为0.2kg的小球,另一端固定在O点,现将轻杆拉直至水平位置,然后给小球一沿着平板并与轻杆垂直的初速度v0=3.0m/s,g=10m/s2,则( )| A. | 此时小球的加速度大小为30m/s2 | |
| B. | 小球到达最高点时杆的弹力沿斜面向上 | |
| C. | 若增大v0,到达最高点时杆子对小球的弹力一定增大 | |
| D. | 若增大v0,到达最高点时杆子对小球的弹力可能减小 |
9.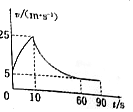 一直升机悬停在停离地1000m的高空,一质量为50kg的跳伞运动员从直升机上跳下,10s后打开降落伞,已知打开降落伞阻力大小与速度大小成正比,将跳伞运动员的运动简化为竖直方向上的直线运动,其v-t图象如图所示,下落90s时跳伞运动员落到地面上,若降落伞的质量不计,则下列说法正确的是( )
一直升机悬停在停离地1000m的高空,一质量为50kg的跳伞运动员从直升机上跳下,10s后打开降落伞,已知打开降落伞阻力大小与速度大小成正比,将跳伞运动员的运动简化为竖直方向上的直线运动,其v-t图象如图所示,下落90s时跳伞运动员落到地面上,若降落伞的质量不计,则下列说法正确的是( )
 一直升机悬停在停离地1000m的高空,一质量为50kg的跳伞运动员从直升机上跳下,10s后打开降落伞,已知打开降落伞阻力大小与速度大小成正比,将跳伞运动员的运动简化为竖直方向上的直线运动,其v-t图象如图所示,下落90s时跳伞运动员落到地面上,若降落伞的质量不计,则下列说法正确的是( )
一直升机悬停在停离地1000m的高空,一质量为50kg的跳伞运动员从直升机上跳下,10s后打开降落伞,已知打开降落伞阻力大小与速度大小成正比,将跳伞运动员的运动简化为竖直方向上的直线运动,其v-t图象如图所示,下落90s时跳伞运动员落到地面上,若降落伞的质量不计,则下列说法正确的是( )| A. | 运动员打开降落伞前,其机械能保持不变 | |
| B. | 整个下落过程,运动员克服阻力做功1.5kJ | |
| C. | 运动员在前60s内的平均速度大小为13.75m/s | |
| D. | 打开降落伞的瞬间,运动员加速度大小为40m/s2 |
6. 一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数($\frac{1}{v}$)图象如图所示.若已知汽车的质量M,则根据图象所给的信息,不能求出的物理量是( )
一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数($\frac{1}{v}$)图象如图所示.若已知汽车的质量M,则根据图象所给的信息,不能求出的物理量是( )
 一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数($\frac{1}{v}$)图象如图所示.若已知汽车的质量M,则根据图象所给的信息,不能求出的物理量是( )
一辆汽车在平直的公路上以某一初速度运动,运动过程中保持恒定的牵引功率,其加速度a和速度的倒数($\frac{1}{v}$)图象如图所示.若已知汽车的质量M,则根据图象所给的信息,不能求出的物理量是( )| A. | 汽车所受到的阻力 | B. | 汽车运动到最大速度所需的时间 | ||
| C. | 汽车的功率 | D. | 汽车行驶的最大速度 |
5. 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )| A. | 轻绳的长度为$\frac{2a}{b}$ | B. | 小球所带电荷量为$\frac{b+mg}{E}$ | ||
| C. | 小球在最高点的最小速度为$\sqrt{\frac{2a}{m}}$ | D. | 小球在最高点的最小速度为$\sqrt{\frac{5a}{m}}$ |
15.将一条形磁铁全部插入闭合线圈中,若第一次全部插入时间为0.2s,第二次全部插入时间为1s,则将条形磁铁第一次插入和第二次插入时线圈单位时间内发热量之比为( )
| A. | 5:1 | B. | 1:5 | C. | 25:1 | D. | 1:1. |
19.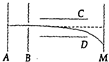 真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由A板从静止开始被同加速电场加速后垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断中正确的是( )
真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由A板从静止开始被同加速电场加速后垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断中正确的是( )
 真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由A板从静止开始被同加速电场加速后垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断中正确的是( )
真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由A板从静止开始被同加速电场加速后垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断中正确的是( )| A. | 三种粒子从B板运动到荧光屏经历的时间相同 | |
| B. | 三种粒子打到荧光屏上的位置相同 | |
| C. | 经过偏转电场,这三种粒子将分成三股粒子束 | |
| D. | 偏转电场的电场力对三种粒子做功之比为1:1:2 |
20.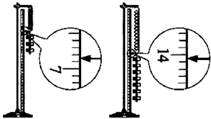 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L7.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L7.
①下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.
测量记录表:
②实验中,L3和L7两个值还没有测定,请你根据如图将这两个测量值填入记录表中.
③为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm d2=L5-L1=6.90cm d3=L6-L2=7.00cm.
请你给出第四个差值d4=L7-L3=7.20cm.
④根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=$\frac{{d}_{1}+{d}_{2}+{d}_{3}+{d}_{4}}{4×4}$,代入数据解得△L=1.74cm.
⑤计算弹簧的劲度系数k=28N/m.(g取9.8m/s2)
 某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L7.
某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L7.①下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是L5和L6.
测量记录表:
| 代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 8.60 | 10.3 | 12.1 |
③为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm d2=L5-L1=6.90cm d3=L6-L2=7.00cm.
请你给出第四个差值d4=L7-L3=7.20cm.
④根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4表示的式子为:△L=$\frac{{d}_{1}+{d}_{2}+{d}_{3}+{d}_{4}}{4×4}$,代入数据解得△L=1.74cm.
⑤计算弹簧的劲度系数k=28N/m.(g取9.8m/s2)
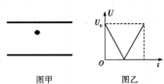 如图甲所示,水平正对放置的两极板间加有按如图乙所示规律变化的电压,电压大小先由U0随时间均匀减小到零,然后又从零随时间均匀增大到U0,开始时极板间某带电微粒处于静止状态,则下列各图能正确描述该微粒的加速度a或速度v随时间t变化规律的是( )
如图甲所示,水平正对放置的两极板间加有按如图乙所示规律变化的电压,电压大小先由U0随时间均匀减小到零,然后又从零随时间均匀增大到U0,开始时极板间某带电微粒处于静止状态,则下列各图能正确描述该微粒的加速度a或速度v随时间t变化规律的是( )