题目内容
4. 如图所示,在水平转台上放一个质量M=2.0kg的木块,它与台面间的最大静摩擦力Ffm=6.0N,绳的一端系住木块,另一端穿过转台的中心孔O(为光滑的)悬吊一质量m=1.0kg的小球,当转台以ω=5.0rad/s的角速度转动时,欲使木块相对转台静止,则它到O孔的距离不可能是( )
如图所示,在水平转台上放一个质量M=2.0kg的木块,它与台面间的最大静摩擦力Ffm=6.0N,绳的一端系住木块,另一端穿过转台的中心孔O(为光滑的)悬吊一质量m=1.0kg的小球,当转台以ω=5.0rad/s的角速度转动时,欲使木块相对转台静止,则它到O孔的距离不可能是( )| A. | 6 cm | B. | 15 cm | C. | 30 cm | D. | 34 cm |
分析 质量为M的物体靠绳子的拉力和静摩擦力的合力提供向心力,当摩擦力达到最大静摩擦力且指向圆心时,转动半径最大,当摩擦力达到最大静摩擦力且方向背离圆心时,转动半径最小,根据向心力公式列式即可求解距离范围,再进行选择
解答 解:M在水平面内转动时,平台对M的支持力与Mg相平衡,拉力与平台对M的静摩擦力的合力提供向心力.
设M到转台中心的距离为R,M以角速度ω转动所需向心力为Mω2R,
若Mω2R=T=mg,此时平台对M的摩擦力为零.
若R1>R,Mω2R1>mg,平台对M的摩擦力方向向左,由牛顿第二定律:
f+mg=Mω2R1,
当f为最大值fm时,R1最大.
所以,M到转台的最大距离为:R1=$\frac{{F}_{fm}+mg}{m{ω}^{2}}=\frac{6+10}{2×{5}^{2}}$m=0.32m
若R2<R,Mω2R2<mg,平台对M的摩擦力水平向右,由牛顿第二定律.
mg-fm=Mω2R2
f=μMg时,R2最小,最小值为:R2=0.08m.
故木块至O的距离R的范围为:0.08m≤R≤0.32m,所以AD不可能,BC可能.
因选不可能的,故选:AD
点评 本题是圆周运动中临界问题,抓住当M恰好相对此平面滑动时静摩擦力达到最大,由牛顿第二定律求解半径的取值范围

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
14.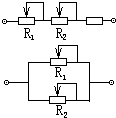 在电子仪器中.常用两个阻值不同的电位器(可变电阻)调节电路中的电流,一个做粗调(电流改变量大)一个做细调(电流改变量小)现连成如图所示两种方式已知R1>R2,则( )
在电子仪器中.常用两个阻值不同的电位器(可变电阻)调节电路中的电流,一个做粗调(电流改变量大)一个做细调(电流改变量小)现连成如图所示两种方式已知R1>R2,则( )
 在电子仪器中.常用两个阻值不同的电位器(可变电阻)调节电路中的电流,一个做粗调(电流改变量大)一个做细调(电流改变量小)现连成如图所示两种方式已知R1>R2,则( )
在电子仪器中.常用两个阻值不同的电位器(可变电阻)调节电路中的电流,一个做粗调(电流改变量大)一个做细调(电流改变量小)现连成如图所示两种方式已知R1>R2,则( )| A. | 串联时,R1做粗调 | B. | 串联时,R1做细调 | C. | 并联时,R1做粗调 | D. | 并联时,R1做细调 |
15.有四个运动的物体A、B、C、D,物体A、B运动的x-t图象如图①所示;物体C、D从同一地点沿同一方向运动的v-t图象如图②所示.根据图象做出的以下判断中正确的是( ) 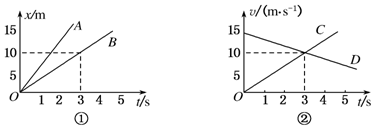
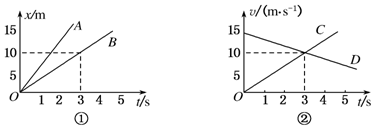
| A. | 物体A和B均做匀速直线运动,且A的速度比B更大 | |
| B. | 在0~3 s的时间内,物体B运动的位移为10 m | |
| C. | t=3 s时,物体C追上物体D | |
| D. | t=3 s时,物体C与物体D之间有最大间距 |
12.质量为m1=2kg,m2=5kg的两静止小车压缩一条轻弹簧后放在光滑的水平面上,放手后把小车弹开.今测得m2受到的冲量是10N•s,则在此过程中,m1的动量的变化量是( )
| A. | 2 kg•m/s | B. | -2 kg•m/s | C. | 10 kg•m/s | D. | -10 kg•m/s |
9.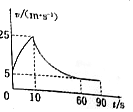 一直升机悬停在停离地1000m的高空,一质量为50kg的跳伞运动员从直升机上跳下,10s后打开降落伞,已知打开降落伞阻力大小与速度大小成正比,将跳伞运动员的运动简化为竖直方向上的直线运动,其v-t图象如图所示,下落90s时跳伞运动员落到地面上,若降落伞的质量不计,则下列说法正确的是( )
一直升机悬停在停离地1000m的高空,一质量为50kg的跳伞运动员从直升机上跳下,10s后打开降落伞,已知打开降落伞阻力大小与速度大小成正比,将跳伞运动员的运动简化为竖直方向上的直线运动,其v-t图象如图所示,下落90s时跳伞运动员落到地面上,若降落伞的质量不计,则下列说法正确的是( )
 一直升机悬停在停离地1000m的高空,一质量为50kg的跳伞运动员从直升机上跳下,10s后打开降落伞,已知打开降落伞阻力大小与速度大小成正比,将跳伞运动员的运动简化为竖直方向上的直线运动,其v-t图象如图所示,下落90s时跳伞运动员落到地面上,若降落伞的质量不计,则下列说法正确的是( )
一直升机悬停在停离地1000m的高空,一质量为50kg的跳伞运动员从直升机上跳下,10s后打开降落伞,已知打开降落伞阻力大小与速度大小成正比,将跳伞运动员的运动简化为竖直方向上的直线运动,其v-t图象如图所示,下落90s时跳伞运动员落到地面上,若降落伞的质量不计,则下列说法正确的是( )| A. | 运动员打开降落伞前,其机械能保持不变 | |
| B. | 整个下落过程,运动员克服阻力做功1.5kJ | |
| C. | 运动员在前60s内的平均速度大小为13.75m/s | |
| D. | 打开降落伞的瞬间,运动员加速度大小为40m/s2 |
5. 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )| A. | 轻绳的长度为$\frac{2a}{b}$ | B. | 小球所带电荷量为$\frac{b+mg}{E}$ | ||
| C. | 小球在最高点的最小速度为$\sqrt{\frac{2a}{m}}$ | D. | 小球在最高点的最小速度为$\sqrt{\frac{5a}{m}}$ |
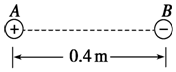 如图所示,在一条直线上有两个相距0.4m的点电荷A、B,A带电荷量+Q,B带电荷量-9Q.现引入第三个点电荷C,恰好使三个点电荷处于平衡状态,问:C应带什么性质的电荷?应放于何处?所带电荷量为多少?
如图所示,在一条直线上有两个相距0.4m的点电荷A、B,A带电荷量+Q,B带电荷量-9Q.现引入第三个点电荷C,恰好使三个点电荷处于平衡状态,问:C应带什么性质的电荷?应放于何处?所带电荷量为多少?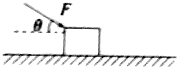 一质量为m的物体放在水平面上,物体和水平面之间的动摩擦因数为μ,用一个与水平方向成θ角的斜向下推力推这个物体,使之在水平面上做匀速直线运动,如图所示,求力F的大小.
一质量为m的物体放在水平面上,物体和水平面之间的动摩擦因数为μ,用一个与水平方向成θ角的斜向下推力推这个物体,使之在水平面上做匀速直线运动,如图所示,求力F的大小.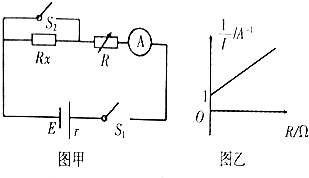 某同学为了精确测量某一阻值约为100Ω的电阻Rx,设计了如图甲所示的电路图,实验台上摆放有以下器材:
某同学为了精确测量某一阻值约为100Ω的电阻Rx,设计了如图甲所示的电路图,实验台上摆放有以下器材: