题目内容
14.用电器电阻值为R距交变电源L,输电线电流为I,电阻率为ρ,要求输电线上电压降不超过U.则输电线截面积最小值为( )| A. | $\frac{ρL}{R}$ | B. | $\frac{2ρLI}{U}$ | C. | $\frac{U}{ρLI}$ | D. | $\frac{2UL}{ρI}$ |
分析 根据欧姆定律可求和电阻的最小值,再由电阻定律即可求出输电导线的横截面积,从而即可求解.
解答 解:根据欧姆定律得:R=$\frac{U}{I}$,
根据电阻定律有:R=2$\frac{ρL}{S}$,
解得:S=$\frac{2ρLI}{U}$.故B正确,A、C、D错误.
故选:B.
点评 解决本题的关键掌握电阻定律和欧姆定律,注意导线输电导线应为两条,故长度为距离的2倍.

练习册系列答案
相关题目
12.质量为m1=2kg,m2=5kg的两静止小车压缩一条轻弹簧后放在光滑的水平面上,放手后把小车弹开.今测得m2受到的冲量是10N•s,则在此过程中,m1的动量的变化量是( )
| A. | 2 kg•m/s | B. | -2 kg•m/s | C. | 10 kg•m/s | D. | -10 kg•m/s |
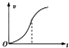
5. 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )| A. | 轻绳的长度为$\frac{2a}{b}$ | B. | 小球所带电荷量为$\frac{b+mg}{E}$ | ||
| C. | 小球在最高点的最小速度为$\sqrt{\frac{2a}{m}}$ | D. | 小球在最高点的最小速度为$\sqrt{\frac{5a}{m}}$ |
19.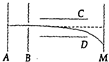 真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由A板从静止开始被同加速电场加速后垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断中正确的是( )
真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由A板从静止开始被同加速电场加速后垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断中正确的是( )
 真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由A板从静止开始被同加速电场加速后垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断中正确的是( )
真空中的某装置如图所示,其中平行金属板A、B之间有加速电场,C、D之间有偏转电场,M为荧光屏.今有质子、氘核和α粒子均由A板从静止开始被同加速电场加速后垂直于电场方向进入偏转电场,最后打在荧光屏上.已知质子、氘核和α粒子的质量之比为1:2:4,电荷量之比为1:1:2,则下列判断中正确的是( )| A. | 三种粒子从B板运动到荧光屏经历的时间相同 | |
| B. | 三种粒子打到荧光屏上的位置相同 | |
| C. | 经过偏转电场,这三种粒子将分成三股粒子束 | |
| D. | 偏转电场的电场力对三种粒子做功之比为1:1:2 |
3.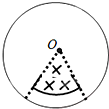 如图,一均匀金属圆盘绕通过其圆心且与盘面垂直的轴顺时针匀速转动.现施加一垂直穿过圆盘的有界匀强磁场,圆盘开始减速.在圆盘减速过程中,以下说法正确的是( )
如图,一均匀金属圆盘绕通过其圆心且与盘面垂直的轴顺时针匀速转动.现施加一垂直穿过圆盘的有界匀强磁场,圆盘开始减速.在圆盘减速过程中,以下说法正确的是( )
 如图,一均匀金属圆盘绕通过其圆心且与盘面垂直的轴顺时针匀速转动.现施加一垂直穿过圆盘的有界匀强磁场,圆盘开始减速.在圆盘减速过程中,以下说法正确的是( )
如图,一均匀金属圆盘绕通过其圆心且与盘面垂直的轴顺时针匀速转动.现施加一垂直穿过圆盘的有界匀强磁场,圆盘开始减速.在圆盘减速过程中,以下说法正确的是( )| A. | 处于磁场中的圆盘部分,靠近圆心处电势高 | |
| B. | 所加磁场越强越易使圆盘停止转动 | |
| C. | 若所加磁场反向,圆盘将加速转动 | |
| D. | 若所加磁场穿过整个圆盘,圆盘将匀速转动 |
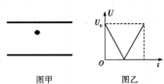 如图甲所示,水平正对放置的两极板间加有按如图乙所示规律变化的电压,电压大小先由U0随时间均匀减小到零,然后又从零随时间均匀增大到U0,开始时极板间某带电微粒处于静止状态,则下列各图能正确描述该微粒的加速度a或速度v随时间t变化规律的是( )
如图甲所示,水平正对放置的两极板间加有按如图乙所示规律变化的电压,电压大小先由U0随时间均匀减小到零,然后又从零随时间均匀增大到U0,开始时极板间某带电微粒处于静止状态,则下列各图能正确描述该微粒的加速度a或速度v随时间t变化规律的是( )
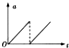


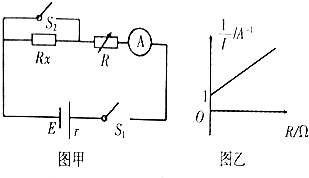 某同学为了精确测量某一阻值约为100Ω的电阻Rx,设计了如图甲所示的电路图,实验台上摆放有以下器材:
某同学为了精确测量某一阻值约为100Ω的电阻Rx,设计了如图甲所示的电路图,实验台上摆放有以下器材: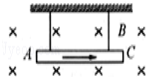 如图所示,一根质量为m的金属棒AC用长短相同的软线悬挂在磁感应强度为B的匀强磁场中,通入A到C方向的电流时,AC受到的安培力方向向上 (选填“上”、“下”、“左”、“右”),若改变电流的方向,悬线受到的张力将变大(选填“变大”、“变小”或“不变”),若同时改变电流方向和磁场方向,金属棒受到的安培力方向不变(选填“改变”或“不变”)
如图所示,一根质量为m的金属棒AC用长短相同的软线悬挂在磁感应强度为B的匀强磁场中,通入A到C方向的电流时,AC受到的安培力方向向上 (选填“上”、“下”、“左”、“右”),若改变电流的方向,悬线受到的张力将变大(选填“变大”、“变小”或“不变”),若同时改变电流方向和磁场方向,金属棒受到的安培力方向不变(选填“改变”或“不变”)