题目内容
4.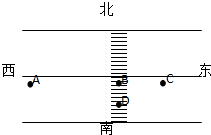 在某市区内,一辆汽车在平直的马路上以速度vA向东匀速行驶,一位观光游客正由南向北从斑马线上横过马路.汽车司机在A处发现前方有危险(游客正在D处),经t0=0.5s作出反应后紧急刹车,但仍将正在步行到B处的游客撞伤,而汽车仍保持匀减速直线运动到C处停下,如图所示.为了判断汽车司机是否超速行驶,警方用一性能完全相同的汽车以法定最高速度v0=12m/s行驶在这同一地段,由于事前有思想准备,司机在A处即紧急刹车,经12m停下.在事故现场测得AB=19.5m,BC=6.75m,BD=3.9m.问:
在某市区内,一辆汽车在平直的马路上以速度vA向东匀速行驶,一位观光游客正由南向北从斑马线上横过马路.汽车司机在A处发现前方有危险(游客正在D处),经t0=0.5s作出反应后紧急刹车,但仍将正在步行到B处的游客撞伤,而汽车仍保持匀减速直线运动到C处停下,如图所示.为了判断汽车司机是否超速行驶,警方用一性能完全相同的汽车以法定最高速度v0=12m/s行驶在这同一地段,由于事前有思想准备,司机在A处即紧急刹车,经12m停下.在事故现场测得AB=19.5m,BC=6.75m,BD=3.9m.问:(1)该肇事汽车是否超速?刹车时的加速度多大?
(2)游客横过马路的步行速度多大?
分析 (1)先由试验车的匀加速过程求汽车的加速度即是肇事车的加速度,再由位移公式求肇事车刹车时的速度;(2)先求汽车由A到B匀减速运动时间,再求行人的速度.
解答 解:(1)对于实验汽车,由$0-{{v}_{0}}^{2}=2{ax}_{0}$得,
$a=-\frac{{{v}_{0}}^{2}}{2{x}_{0}}=-\frac{{12}^{2}}{2×12}m/{s}^{2}=-6m/{s}^{2}$
由${x}_{AC}={v}_{A}{t}_{0}+\frac{0-{{v}_{A}}^{2}}{2a}$,即$19.5m+6.75m={v}_{A}×0.5s+\frac{0-{{v}_{A}}^{2}}{2×(-6m/{s}^{2})}$得,
vA=15m/s(vA=-21m/s舍去)>12m/s,故该车超速行驶.
(2)设汽车由A到B匀减速运动时间t1,
则${x}_{AB}={v}_{A}{t}_{0}+{v}_{A}{t}_{1}+\frac{1}{2}{{at}_{1}}^{2}$,即$19.5m=15m/s×0.5m+15m/s×{t}_{1}+\frac{1}{2}×(-6m/s)×{{t}_{1}}^{2}$得,
t1=1s,
所以${v}_{人}=\frac{{x}_{BD}}{{t}_{0}+{t}_{1}}=\frac{3.9m}{0.5s+1s}=2.6m/s$
答:(1)该肇事汽车超速,刹车时的加速度为6m/s2.
(2)游客横过马路的步行速度为2.6m/s.
点评 本题考查了匀变速直线运动的规律,第一问解题的关键先由试验车的匀加速过程求汽车的加速度即是肇事车的加速度,再由位移公式求肇事车刹车时的速度;第二问先求汽车由A到B匀减速运动时间,再求行人的速度.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案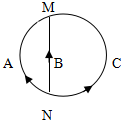 三个质点A、B、C的运动轨迹如图所示,三个质点同时从N点出发,分别做速度大小不变的运动,同时到达M点,下列说法中正确的是( )
三个质点A、B、C的运动轨迹如图所示,三个质点同时从N点出发,分别做速度大小不变的运动,同时到达M点,下列说法中正确的是( )| A. | 三个质点从N点到M点的平均速度的大小相等,方向相同 | |
| B. | 三个质点从N到M的平均速度大小相等,但方向不同相同 | |
| C. | 到达M点时的速率一定是A的最大 | |
| D. | B质点从N到M的平均速度方向与任意时刻瞬时速度方向相同 |
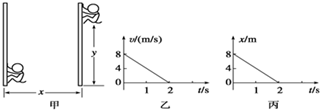
| A. | 猴子的运动轨迹为直线 | |
| B. | 猴子在2 s内做匀变速曲线运动 | |
| C. | t=0时猴子的速度大小为8 m/s | |
| D. | 猴子在2 s内的加速度大小为4 m/s2 |
| A. | 某航班于14时30分从北京起飞 | |
| B. | 中央电视台的新闻联播节目于19时开播 | |
| C. | 某短跑运动员用11.5秒跑完100米 | |
| D. | 在某场足球赛中,甲队于开赛10分后攻入一球 |
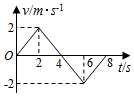 若一质点从t=0开始由原点出发,其v-t图象如图所示,则该质点( )
若一质点从t=0开始由原点出发,其v-t图象如图所示,则该质点( )| A. | 在前8s内做匀变速直线运动 | |
| B. | 在2-6s内做匀变速直线运动 | |
| C. | 6s末的速度大小为2m/s,方向与规定的正方向相反 | |
| D. | 4-6s内与6-8s内的速度方向相反 |

| A. | 船渡河的最短时间是60s | |
| B. | 若船最短时间渡河,船头始终与河岸垂直 | |
| C. | 船在河水中航行的轨迹是一条直线 | |
| D. | 船渡河的最短路程可能为300m |
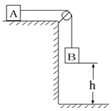 如图所示,mA=4kg,A放在动摩擦因数μ=0.2的水平桌面上,mB=1kg,B与地相距h=0.8m,A、B均从静止开始运动,设A距桌子边缘足够远,g取10m/s2,求:
如图所示,mA=4kg,A放在动摩擦因数μ=0.2的水平桌面上,mB=1kg,B与地相距h=0.8m,A、B均从静止开始运动,设A距桌子边缘足够远,g取10m/s2,求: