题目内容
13.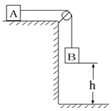 如图所示,mA=4kg,A放在动摩擦因数μ=0.2的水平桌面上,mB=1kg,B与地相距h=0.8m,A、B均从静止开始运动,设A距桌子边缘足够远,g取10m/s2,求:
如图所示,mA=4kg,A放在动摩擦因数μ=0.2的水平桌面上,mB=1kg,B与地相距h=0.8m,A、B均从静止开始运动,设A距桌子边缘足够远,g取10m/s2,求:(1)B落地时的速度;
(2)B落地后,A在桌面滑行多远才静止.
分析 (1)减小的重力势能转化为AB的动能和A克服摩擦力做功产生的内能,根据能量守恒定律求解B落到地面时的速度.
(2)B落地后(不反弹),A在水平面上继续滑行,根据动能定理求解A滑行的距离.
解答 解:(1)以A、B物体构成的系统为对象,B物体所受重力mBg做正功,mA物体所受的摩擦力对系统做负功,由动能定理得:
mBgh-μmAgh=$\frac{1}{2}$(mA+mB)v2
即:v=0.8m/s;
(2)B落地后,A以v=1.6m/s初速度继续向前运动,克服摩擦力做功最后停下,根据动能定理得:
μmAgs′=$\frac{1}{2}$mAv2
解得:s′=$\frac{{v}^{2}}{2μg}$=$\frac{0.{8}^{2}}{2×0.2×10}$=0.16m;
答:(1)B落到地面时的速度为0.8m/s;
(2)B落地后,A在桌面上能继续滑行0.16m才能静止下来.
点评 本题是连接体问题,采用能量守恒定律研究,也可以运用动能定理、或牛顿运动定律和运动公式结合研究.关键在于正确分析受力以及能量的转化规律.

练习册系列答案
相关题目
3. 如图所示,“超级巴士”是传统巴士的变革,长15英尺,可以搭载23名乘客,最大速度可以达到每小时255公里.如果四辆相同的“超级巴士”排成一列由静止开始加速,某人站在第一辆“超级巴士”车头的一侧.不计相邻两辆“超级巴士”之间的距离,若第二辆“超级巴士”完全经过此人的时间是($\sqrt{2}$-1)s,那么第四辆“超级巴士”完全经过此人的是时间是( )
如图所示,“超级巴士”是传统巴士的变革,长15英尺,可以搭载23名乘客,最大速度可以达到每小时255公里.如果四辆相同的“超级巴士”排成一列由静止开始加速,某人站在第一辆“超级巴士”车头的一侧.不计相邻两辆“超级巴士”之间的距离,若第二辆“超级巴士”完全经过此人的时间是($\sqrt{2}$-1)s,那么第四辆“超级巴士”完全经过此人的是时间是( )
 如图所示,“超级巴士”是传统巴士的变革,长15英尺,可以搭载23名乘客,最大速度可以达到每小时255公里.如果四辆相同的“超级巴士”排成一列由静止开始加速,某人站在第一辆“超级巴士”车头的一侧.不计相邻两辆“超级巴士”之间的距离,若第二辆“超级巴士”完全经过此人的时间是($\sqrt{2}$-1)s,那么第四辆“超级巴士”完全经过此人的是时间是( )
如图所示,“超级巴士”是传统巴士的变革,长15英尺,可以搭载23名乘客,最大速度可以达到每小时255公里.如果四辆相同的“超级巴士”排成一列由静止开始加速,某人站在第一辆“超级巴士”车头的一侧.不计相邻两辆“超级巴士”之间的距离,若第二辆“超级巴士”完全经过此人的时间是($\sqrt{2}$-1)s,那么第四辆“超级巴士”完全经过此人的是时间是( )| A. | (2-$\sqrt{3}$)s | B. | $\sqrt{2}$s | C. | ($\sqrt{2}$-1)s | D. | 1s |
1.关于匀速直线运动,以下说法正确的是( )
| A. | 只要速度大小不变,就是匀速直线运动 | |
| B. | 若物体每秒内的位移相同,则一定是匀速直线运动 | |
| C. | 速度大小不变的直线运动一定是匀速直线运动 | |
| D. | 速度大小不变的单向直线运动一定是匀速直线运动 |
18.目前,在居室装修中经常用到花岗岩、大理石等装饰材料,这些材料都不同程度地含有放射性元素,下列有关放射性元素的说法中正确的是( )
| A. | β射线与γ射线一样都是电磁波,但穿透本领远比γ射线弱 | |
| B. | 氡的半衰期为3.8天,4个氡原子核经过7.6天后一定只剩下1个氡原子核 | |
| C. | ${\;}_{92}^{238}$U哀变成${\;}_{82}^{206}$Pb要经过6次α衰变和6次β衰变 | |
| D. | 放射性元素发生β衰变所释放的电子是原子核内的中子转化为质子时产生的 |
2.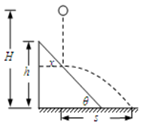 如图所示,已知倾角为θ=45°、高为h的斜面固定在水平地面上.一小球从高为H(h<H<$\frac{5}{4}$h)处自由下落,与斜面做无能量损失的碰撞后水平抛出,小球自由下落的落点距斜面左侧的水平距离x满足一定条件时,小球能直接落到水平地面上,下列说法正确的是( )
如图所示,已知倾角为θ=45°、高为h的斜面固定在水平地面上.一小球从高为H(h<H<$\frac{5}{4}$h)处自由下落,与斜面做无能量损失的碰撞后水平抛出,小球自由下落的落点距斜面左侧的水平距离x满足一定条件时,小球能直接落到水平地面上,下列说法正确的是( )
 如图所示,已知倾角为θ=45°、高为h的斜面固定在水平地面上.一小球从高为H(h<H<$\frac{5}{4}$h)处自由下落,与斜面做无能量损失的碰撞后水平抛出,小球自由下落的落点距斜面左侧的水平距离x满足一定条件时,小球能直接落到水平地面上,下列说法正确的是( )
如图所示,已知倾角为θ=45°、高为h的斜面固定在水平地面上.一小球从高为H(h<H<$\frac{5}{4}$h)处自由下落,与斜面做无能量损失的碰撞后水平抛出,小球自由下落的落点距斜面左侧的水平距离x满足一定条件时,小球能直接落到水平地面上,下列说法正确的是( )| A. | 小球落到地面上的速度大小为$\sqrt{2gH}$ | |
| B. | x应满足的条件是H-h<x<h | |
| C. | x应满足的条件是h-0.8H<x<h | |
| D. | x取不同值时,小球在空中运动的时间不变 |
3. 如图所示,顶端装有定滑轮的斜面体放在粗糙水平面上,A、B两物体通过细绳相连,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦).现用水平向右的力F作用于物体B上,将物体B缓慢拉高一定的距离,此过程中斜面体与物体A仍然保持静止.在此过程中( )
如图所示,顶端装有定滑轮的斜面体放在粗糙水平面上,A、B两物体通过细绳相连,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦).现用水平向右的力F作用于物体B上,将物体B缓慢拉高一定的距离,此过程中斜面体与物体A仍然保持静止.在此过程中( )
 如图所示,顶端装有定滑轮的斜面体放在粗糙水平面上,A、B两物体通过细绳相连,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦).现用水平向右的力F作用于物体B上,将物体B缓慢拉高一定的距离,此过程中斜面体与物体A仍然保持静止.在此过程中( )
如图所示,顶端装有定滑轮的斜面体放在粗糙水平面上,A、B两物体通过细绳相连,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦).现用水平向右的力F作用于物体B上,将物体B缓慢拉高一定的距离,此过程中斜面体与物体A仍然保持静止.在此过程中( )| A. | 水平力F一定变小 | |
| B. | 斜面体所受地面的支持力一定变大 | |
| C. | 物体A所受斜面体的摩擦力一定变大 | |
| D. | 地面对斜面体的摩擦力一定变大 |
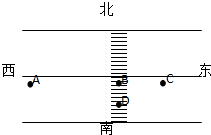 在某市区内,一辆汽车在平直的马路上以速度vA向东匀速行驶,一位观光游客正由南向北从斑马线上横过马路.汽车司机在A处发现前方有危险(游客正在D处),经t0=0.5s作出反应后紧急刹车,但仍将正在步行到B处的游客撞伤,而汽车仍保持匀减速直线运动到C处停下,如图所示.为了判断汽车司机是否超速行驶,警方用一性能完全相同的汽车以法定最高速度v0=12m/s行驶在这同一地段,由于事前有思想准备,司机在A处即紧急刹车,经12m停下.在事故现场测得AB=19.5m,BC=6.75m,BD=3.9m.问:
在某市区内,一辆汽车在平直的马路上以速度vA向东匀速行驶,一位观光游客正由南向北从斑马线上横过马路.汽车司机在A处发现前方有危险(游客正在D处),经t0=0.5s作出反应后紧急刹车,但仍将正在步行到B处的游客撞伤,而汽车仍保持匀减速直线运动到C处停下,如图所示.为了判断汽车司机是否超速行驶,警方用一性能完全相同的汽车以法定最高速度v0=12m/s行驶在这同一地段,由于事前有思想准备,司机在A处即紧急刹车,经12m停下.在事故现场测得AB=19.5m,BC=6.75m,BD=3.9m.问: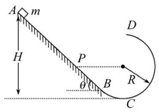 如图所示,AB是倾角θ为45°的直轨道,CD是半径R=0.4m的圆弧轨道,它们通过一段曲面BC平滑相接,整个轨道处于竖直平面内且处处光滑.一个质量m=1kg的物体(可以看作质点)从高H的地方由静止释放,结果它从圆弧最高点D点飞出,垂直斜面击中P点.已知P点与圆弧的圆心O等高.g取10m/s2.求:
如图所示,AB是倾角θ为45°的直轨道,CD是半径R=0.4m的圆弧轨道,它们通过一段曲面BC平滑相接,整个轨道处于竖直平面内且处处光滑.一个质量m=1kg的物体(可以看作质点)从高H的地方由静止释放,结果它从圆弧最高点D点飞出,垂直斜面击中P点.已知P点与圆弧的圆心O等高.g取10m/s2.求: