题目内容
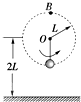
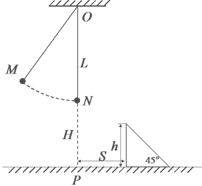
如图所示,质量为m=1kg的小球用线长l=1m的细线拴住,细绳上端固定在O点,当小球从图示M点释放后摆到悬点O的正下方N点时,细线恰好被拉断,此后小球刚好能无碰撞地从置于地面上倾角为45°的斜面滑下,已知斜面高度h=0.4m,斜面左端离O点正下方的P点水平距离S=0.4m,不计空气阻力,求:
(1)N点距离地面的高度H;
(2)细绳能承受的最大拉力.
(1)N点距离地面的高度H;
(2)细绳能承受的最大拉力.

(1)小球无碰撞进入斜面,速度关系:vy=v0tan45o,
又vy=gt
位移关系:水平位移s=v0t,竖直位移y=
gt2
解得:v0=2m/s,t=0.2s,y=0.2m
那么H=h+y=0.6m
(2)小球在N点时绳子的拉力与重力的合力提供向心力:F-mg=m
得:F=m
+mg=14N
答:(1)N点距离地面的高度H为0.6m;(2)细绳能承受的最大拉力为14N.
又vy=gt
位移关系:水平位移s=v0t,竖直位移y=
| 1 |
| 2 |
解得:v0=2m/s,t=0.2s,y=0.2m
那么H=h+y=0.6m
(2)小球在N点时绳子的拉力与重力的合力提供向心力:F-mg=m
| ||
| L |
得:F=m
| ||
| L |
答:(1)N点距离地面的高度H为0.6m;(2)细绳能承受的最大拉力为14N.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目