题目内容
10．
如图所示，两个匀强磁场横截面分别为圆形和正方形，内部磁感应强度大小均为B，方向均垂直于纸面向里，圆的直径D等于正方形的边长．两个完全相同的带电粒子同是以相同的速度v分别飞入两个磁场区域，速度方向均与磁场方向垂直，进入圆形区域的带电粒子速度方向对准了圆心，进入正方形区域的带电粒子是沿一边的中心无助于垂直于边界线进入的，则（ ）| A． | 两个带电粒子在磁场中运动的半径一定相同 | |
| B． | 两个带电粒子在磁场中运动的时间一定相同 | |
| C． | 两个带电粒子可能同时飞离磁场 | |
| D． | 进入圆形区域的带电粒子可能先飞离磁场 |
分析 粒子在磁场中做匀速圆周运动，由洛伦兹力提供向心力，根据半径公式判断半径是否相同．运动时间的判断可以根据粒子转过的圆心角的大小；比较哪个磁场粒子先出磁场，可以做出多个轨迹比较．
解答 解：A：粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力$qvB=m\frac{{v}^{2}}{R}$，R=$\frac{mv}{qB}$，两过程粒子速度v相同，所以半径相同，故A正确．
B、C、D：粒子在磁场中的可能运动情况如图所示，粒子从O点水平进入由于它们进入圆形磁场和正方形磁场的轨道半径、速度是相同的，把圆形磁场和矩形磁场的边界放到同一位置如图所示，由图可以看出进入磁场区域的粒子的轨迹1，先出圆形磁场，再出正方形磁场，此时运动时间不同；进入磁场区域的粒子的轨迹2，同时从圆形与正方形边界处磁场，此时运动时间相同；进入磁场区域的粒子的轨迹3，先出圆形磁场，再出正方形磁场，此时运动时间不同；所以粒子不会先出正方形的磁场，即进入圆形区域的电子一定不会后飞离磁场，故CD正确，B错误．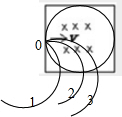
故选：ACD．
点评 解决本题的关键掌握粒子在磁场中的半径公式和周期公式，掌握求解运动的时间的方法，本题的难点在于能否想到在同一个图象中做出多个轨迹进行比较哪个先出磁场．
练习册系列答案
相关题目
20．如图，人站在自动扶梯上不动，随扶梯匀速上升的过程中（ ）
| A． | 人克服重力做功，重力势能不变 | |
| B． | 支持力对人做正功，人的动能增加 | |
| C． | 合外力对人不做功，人的动能不变 | |
| D． | 合外力对人不做功，人的机械能不变 |
如图所示，两平行的光滑金属导轨间距为L且置于磁感应强度为B的匀强磁场中，磁场方向垂直于导轨平面，导轨一端MN间接一电阻R，PQ端接一对平行金属板，导体棒ab置于导轨上，其电阻Rab=3R，导轨电阻不计，平行金属板间距为d，其中磁感应强度也为B，令导体棒向右以速度v做匀速运动时，有一液滴恰能在平行金属板间做半径为r的匀速圆周运动，速率也为v，求：
15．
如图所示，质量为m、带正电的小球，在竖直向上的匀强电场中的A点由静止开始释放，以$\frac{1}{2}$g（g为重力加速度）的加速度竖直向下下降高度为h到达B点．空气阻力不计，则在此过程中，下列说法正确的是（ ）
如图所示，质量为m、带正电的小球，在竖直向上的匀强电场中的A点由静止开始释放，以$\frac{1}{2}$g（g为重力加速度）的加速度竖直向下下降高度为h到达B点．空气阻力不计，则在此过程中，下列说法正确的是（ ）| A． | 小球重力势能减少了$\frac{1}{2}$mgh | B． | 小球动能增加了mgh | ||
| C． | 小球克服电场力做功为$\frac{1}{2}$mgh | D． | 小球机械能减少了$\frac{1}{2}$mgh |
水平面内固定一U形光滑金属导轨，轨道宽d=2m，导轨的左端接有R=0.3Ω的电阻，导轨上放一阻值为R0=0.1Ω，m=0.1kg的导体棒ab，其余电阻不计，导体棒ab用水平轻线通过定滑轮连接处于水平地面上质量M=0.3kg的重物，空间有竖直向上的匀强磁场，如图所示．已知t=0时，B=1T，L=1m，此时重物上方的连线刚刚被拉直．从t=0开始，磁感应强度以 0.1T/s均匀增加，取g=10m/s2．求：