题目内容
【题目】如图所示，一束宽度为d的平行光射向截面为正三角形的玻璃三棱镜，入射光与AB界面夹角为45°，玻璃的折射率n= 
，光束通过三棱镜后到达与BC界面平行的光屏PQ，求光屏PQ上光斑的宽度D．
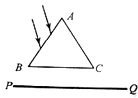
【答案】解：作出光路图如图所示．设AB面的入射角为θ，折射角为γ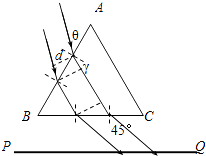
由折射定律得 n= 
得 γ=30°
光线射到BC边时由几何关系可知入射角 γ′=30°
由折射定律得 n= 
得 θ′=45°
由几何关系光斑的宽度
D= 
得 D= 
d
答：光屏PQ上光斑的宽度D是 d
【解析】光屏PQ上光斑是平行通过三棱镜两次折射形成，根据折射定律求出两次折射的折射角，画出光路图，由几何关系求解光屏PQ上光斑的宽度D．
【考点精析】掌握光的折射是解答本题的根本，需要知道光由一种介质射入另一种介质时，在两种介质的界面上将发生光的传播方向改变的现象叫光的折射．
练习册系列答案
初中暑期衔接系列答案
相关题目
