题目内容
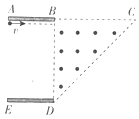
【题目】如图所示,轨道倪a、b、c在同一竖直平面内,其中a是末端水平(可看做与D重合)的光滑圆弧轨道,b是半径为r=2m的光滑半圆形轨道且直径DF沿竖直方向,水平轨道c上静止放置着相距l=1.0m的物块B和C,B位于F处,现将滑块A从轨道a以上距D点高为H的位置由静止释放,滑块A经D处水平进入轨道b后能沿轨道(内轨)运动,到达F处与物块B正碰,碰后A、B粘在一起向右滑动,并再与C发生正碰.已知A、B、C质量分别为m、m、km,均可看做质点,物块与轨道C的动摩擦因数μ=0.45.(设碰撞时间很短,g取10m/s2)
(1)求H的最小值和H取最小值时,AB整体与C碰撞前瞬间的速度;
(2)若在满足(1)的条件下,碰后瞬间C的速度=2.0m/s,请根据AB整体与C的碰撞过程分析k的取值,并讨论与C碰撞后AB的可能运动方向.
【答案】
(1)解:滑块A从轨道a下滑到达D点的过程中,由机械能守恒定律得:
mgH= ![]() mvD2,
mvD2,
要使滑块A能沿竖直平面内光滑半圆轨道b内侧做圆周运动,在D点应满足:
mg≤ ![]() ,
,
联立并代入数据解得 H≥1m
所以H的最小值为1m.
滑块A从a轨道上H=1m处下滑到达F点的过程,由机械能守恒定律得
mg(H+2r)= ![]()
可得,滑块经过F点的速度 v0=10m/s
A、B碰撞过程,取向右为正方向,由动量守恒定律得
mv0=2mv1.
设AB整体与C碰撞前瞬间的速度为v2.由动能定理得
﹣μ2mgl= ![]() ﹣
﹣ ![]()
联立以上各式解得 v2=4m/s
答:H的最小值是1m,H取最小值时,AB整体与C碰撞前瞬间的速度是 ![]() m/s.
m/s.
(2)若AB整体与C发生非弹性碰撞,由动量守恒定律得
2mv2=(2m+km)v
代入数据解得 k=2
此时AB整体的运动方向与C相同.
若AB整体与C发生弹性碰撞,由动量守恒定律和能量守恒定律得
2mv2=2mv3+kmv
![]() ×2mv22=
×2mv22= ![]() ×2mv32+
×2mv32+ ![]() kmv2
kmv2
解得 v3= ![]() v2,v=
v2,v= ![]() v2
v2
代入数据解得 k=6
此时AB整体的运动方向与C相反.
若AB整体与C发生碰撞后AB整体速度为0,由动量守恒定律得
2mv2=kmv
解得 k=4
综上所述,当2≤k<4时,AB整体的运动方向与C相同.
当k=4时,AB整体的速度为0.
当4<k≤6时,AB整体的运动方向与C相反.
答:当2≤k<4时,AB整体的运动方向与C相同.当k=4时,AB整体的速度为0.当4<k≤6时,AB整体的运动方向与C相反.
【解析】(1)滑块在最高点时,重力提供向心力。滑块下滑过程中满足机械能守恒,求出高度的最小值。碰撞过程中满足动量守恒,根据动量守恒和动能定理,列式求解。
(2)碰撞过程中有动能向其他形式能转化,是非弹性碰撞。根据动量守恒和机械能守恒,联合列式求解。

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案