题目内容
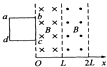
【题目】如图所示,在梯形ACDE内存在沿竖直方向的匀强电场,在等腰直角三角形BCD内同时存在垂直于纸面向外的匀强磁场,BD是一个上端带有小孔的挡板,现有一个质量为m,电荷量大小为q的带电粒子以水平速度v贴近AB边射入匀强电场,且做直线运动,通过小孔射入电磁场(△BCD区域),粒子恰好能以最大的圆周半径偏转并打到B D板上,AB、ED两极板间电势差为U,重力加速度为g.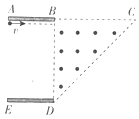
(1)试判断电场方向及BD的长度d;
(2)求磁感应强度.
【答案】
(1)解:粒子在电场中只受竖直方向的重力、电场力作用,沿水平方向做直线运动,故粒子在电场中受力平衡;
重力方向竖直向下,故电场力方向竖直向上,则电场方向竖直向上;
由受力平衡可得: ![]() ,所以,
,所以, ![]() ;
;
答:电场方向竖直向上,BD的长度d为 ![]() ;
;
(2)粒子在电磁场中运动,合外力为洛伦兹力;粒子以最大半径做圆周运动,故粒子运动轨迹与CD边相切,那么由几何关系可得: ![]() ;
;
所以,粒子做圆周运动的半径 ![]() ;
;
由洛伦兹力做向心力可得: ![]() ,所以,
,所以, ![]() ;
;
答:磁感应强度为 ![]() .
.
【解析】(1)带电粒子在电场中做直线运动,结合粒子受力情况进行分析,粒子只能受力平衡重力和电场力等大反向。结合匀强电场电场强度和电势差之间的关系列式求解。
(2)求解带电粒子在匀强磁场中运动的问题,首先根据题意,找出找出圆心,根据几何关系求出半径,再由洛伦兹力提供向心力列式求解。

 阅读快车系列答案
阅读快车系列答案【题目】某实验小组想利用图甲所示的电路研究标有3.5V字样(额定功率字迹不清)的小灯泡的伏安特性.
(1)请根据电路图甲将图乙中所缺的导线补接完整 , 为了保证实验的安全,滑动触头在实验开始前应置于滑动变阻器的最端;(选填“左”或“右”)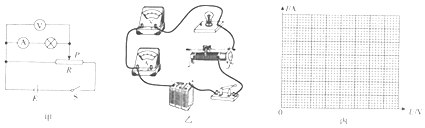
(2)实验得到的8组数据如下表,请在图丙中选择合适的标度作出I﹣U图象;
I/A | 0 | 0.100 | 0.151 | 0.172 | 0.202 | 0.210 | 0.219 | 0.222 |
U/V | 0 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 |
(3)实验中小灯泡两端电压从零变化到额定电压的过程中,小灯泡最大电阻值约为Ω(计算结果保留三位有效数字),系统误差会使测量结果(填“偏大”或“偏小”).