题目内容
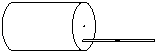
【题目】如图所示,在足够长的水平面A处静止一个长为L=3m,质量M=lkg的木板P,在P右端x=0.8m的B处,有一竖直固定的小挡板,高度略低于木板P,厚度不计,紧靠挡板右侧停放一与P相同木板Q,挡板左侧水平面光滑,右侧与木板Q之间动摩擦因数![]() .现将一质量m=kg可看作质点的铁块轻放在P的左端,木板与铁块之间的动摩擦因数
.现将一质量m=kg可看作质点的铁块轻放在P的左端,木板与铁块之间的动摩擦因数![]() .对铁块施以水平恒力F=5N,使其由静止开始向右运动,木板P与小挡板相碰会立即停下,铁块继续运动,并滑上木板Q,重力加速度g取
.对铁块施以水平恒力F=5N,使其由静止开始向右运动,木板P与小挡板相碰会立即停下,铁块继续运动,并滑上木板Q,重力加速度g取![]() ,求:铁块由静止开始运动到木板Q最右端所用时间.
,求:铁块由静止开始运动到木板Q最右端所用时间.

【答案】2.5s
【解析】试题分析:先分析铁块在P木板上的运动,当木板P与挡板碰后,木板P停止运动,铁块继续滑行到木板Q上,再分析铁块在木板Q上的运动,分别应用整体法和隔离法、牛顿第二定律、运动学公式联立方程求出各个阶段运动的时间,各个阶段运动的时间之和即为所求的总时间.
板块向右运动![]() 过程,以整体为研究对象
过程,以整体为研究对象
由牛顿第二定律得: ![]() 解得:
解得: ![]()
以木板P为研究对象,由牛顿第二定律得: ![]()
又因最大静摩擦力![]() ,则有
,则有![]() ,故整体一起运动
,故整体一起运动
由位移公式得: ![]() 解得:
解得: ![]()
由速度公式得: ![]()
木板P与挡板碰后,木板P停止运动,铁块继续滑行,以铁块为研究对象
由牛顿第二定律得: ![]() 解得:
解得: ![]()
由位移公式得: ![]() 解得:
解得: ![]() 或
或 ![]() (舍去)
(舍去)
由速度公式得: ![]()
铁块运动到木板Q后,以铁块为研究对象
由牛顿第二定律得: ![]() 解得:
解得: ![]()
由位移公式得: ![]()
以木板Q为研究对象,由牛顿第二定律得:
![]() 解得:
解得: ![]()
由位移公式得: ![]()
又![]()
联立解得: ![]()
故铁块由静止开始运动到木板Q最右端所用时间为: ![]()

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目