Question

【题目】如图所示为某透明介质的截面图，截面可看做由四分之一个圆面ABO和一个长方形BCDO组成，AO=2DO=R，一束光线在弧面AB的中点E沿垂直于DC边方向射入，折射光线刚好到达D点，求：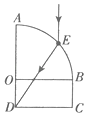

（i）介质对光的折射率；
（ii）光在介质中从E传到D所用的时间（光在真空中的速度为c）．

Answer 1

【答案】解：（i）由于光线圆弧面AB的中点E沿着垂直于DC边射入，

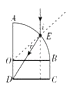
由几何关系，可知，入射角i=45°

ED边的长s= =

由正弦定理，可知，

解得：sinr= =

因此介质对光的折射率n= =

（ii）光从E到D所用的时间，t= = =

答：（i）介质对光的折射率 ；

（ii）光在介质中从E传到D所用的时间 ．

【解析】（1）典型的几何光学试题，先画出光路图，根据几何关系，求出入射角结合三角形三边关系和正玄定理求解。
（2）根据折射率的公式，求出光在介质中的传播速度，再根据匀速直线运动时间和速度关系求解。