题目内容
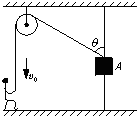
一条河宽s=100m，水流速度v1=3m/s，船在静水速度v2=5m/s，求：
（1）船到达对岸的最短时间tmin
（2）船要以最短距离到达对岸，船与河岸的夹角θ
（3）船以最短距离过河的时间为多少？
（1）船到达对岸的最短时间tmin
（2）船要以最短距离到达对岸，船与河岸的夹角θ
（3）船以最短距离过河的时间为多少？
（1）当以静水中的速度垂直河岸过河的时候渡河时间最短，则知：tmin=
=
s=20s
（2）小船以最短距离过河时，则静水中的速度斜着向上游，合速度垂直河岸，设与河岸的夹角为θ，
则由矢量合成的平行四边形法则解三角形得：cosθ=
=
，
这时船头与河水速度夹角为θ=53°
（3）那么船垂直河岸行驶的速度为v=
m/s=4m/s；
所以渡河时间t=
s=25s；
答：（1）小船过河的最短时间为20s；
（2）要小船以最短距离过河，开船方向与河水速度夹角为53°；
（3）船以最短距离渡河时间为25s．
| d |
| vc |
| 100 |
| 5 |
（2）小船以最短距离过河时，则静水中的速度斜着向上游，合速度垂直河岸，设与河岸的夹角为θ，
则由矢量合成的平行四边形法则解三角形得：cosθ=
| vs |
| vc |
| 3 |
| 5 |
这时船头与河水速度夹角为θ=53°
（3）那么船垂直河岸行驶的速度为v=
| 52-32 |
所以渡河时间t=
| 100 |
| 4 |
答：（1）小船过河的最短时间为20s；
（2）要小船以最短距离过河，开船方向与河水速度夹角为53°；
（3）船以最短距离渡河时间为25s．
练习册系列答案
一线名师口算应用题天天练一本全系列答案
小学学习好帮手系列答案
相关题目
