题目内容
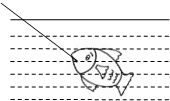
如图所示,长为L=75cm的平底玻璃管,底部放置一可视为质点的小球,现让玻璃管从静止开始以a1=16m/s2的加速度竖直向下运动,经一段时间后小球运动到管口,此时让玻璃管加速度大小减为a2=2.5m/s2,方向不变,空气阻力不计,取g=10m/s2.求:
(1)小球到达管口时小球和玻璃管的速度;
(2)从玻璃管开始运动到小球再次回到玻璃管底部所用的时间.

(1)小球到达管口时小球和玻璃管的速度;
(2)从玻璃管开始运动到小球再次回到玻璃管底部所用的时间.

(1)设玻璃管向下运动的加速度为a,对玻璃管受力分析由牛顿第二定律得,F+mg=ma①
设玻璃球和玻璃管向下运动的位移分别为s1、s2时,玻璃球离开玻璃管,
由题意得,s2-s1=L②
由玻璃球作自由落体运动得,s1=
gt2③
由玻璃管向下加速运动得,s2=
at2④
玻璃球离开玻璃管时,玻璃管的速度v=at⑤
由①~⑤式解得,t=0.5s,
根据速度与时间的关系,则有小球的速度v1=gt=10×0.5m/s=5m/s
玻璃管的速度v2=at=16×0.5m/s=8m/s
(2)根据位移与时间关系,设再次回到玻璃管底部所用的时间为t,
则有:v1t′+
gt′2-(v2t′+
at′2)=L
代入数据,可解得:t′=1.5s
答:(1)时间t为0.5s,小球离开玻璃管时,小球的速度5m/s,玻璃管的速度的大小为8m/s.
(2)小球再次回到玻璃管底部所用的时间1.5s.
设玻璃球和玻璃管向下运动的位移分别为s1、s2时,玻璃球离开玻璃管,
由题意得,s2-s1=L②
由玻璃球作自由落体运动得,s1=
| 1 |
| 2 |
由玻璃管向下加速运动得,s2=
| 1 |
| 2 |
玻璃球离开玻璃管时,玻璃管的速度v=at⑤
由①~⑤式解得,t=0.5s,
根据速度与时间的关系,则有小球的速度v1=gt=10×0.5m/s=5m/s
玻璃管的速度v2=at=16×0.5m/s=8m/s
(2)根据位移与时间关系,设再次回到玻璃管底部所用的时间为t,
则有:v1t′+
| 1 |
| 2 |
| 1 |
| 2 |
代入数据,可解得:t′=1.5s
答:(1)时间t为0.5s,小球离开玻璃管时,小球的速度5m/s,玻璃管的速度的大小为8m/s.
(2)小球再次回到玻璃管底部所用的时间1.5s.

练习册系列答案
相关题目